Великие математики и их открытия. люди, подарившие нам язык вселенной

Открытия Декарта

Коснемся теперь некоторых научных достижений Декарта. В истории математики он занимает весьма видное место. И именно Декарт сыграл решающую роль в становлении современной алгебры тем, что ввёл буквенные символы, обозначил последними буквами латинского алфавита (х, у, z) переменные величины, ввёл нынешнее обозначение степеней, заложил основы теории уравнений. Понятия числа и величины, ранее существовавшие раздельно, тем самым были объединены. Историческое значение Декартовой «геометрии» состоит также в том, что здесь была открыта связь величины и функции, что преобразовало математику. Применение алгебраических методов к геометрическим объектам, введение системы прямолинейных координат означало создание аналитической геометрии, объединяющей геометрические и арифметические величины, которые со времен древнегреческой математики существовали в раздельности. Физические исследования относятся главным образом к механике, оптике и строению Вселенной. Декарт ввёл понятие «силы» (меры) движения (количества движения), подразумевая под ним произведение «величины» тела (массы) на абсолютное значение его скорости, сформулировал закон сохранения движения (количества движения), однако толковал его неправильно, не учитывая, что количество движения является векторной величиной (1664). Исследовал законы удара, впервые четко сформулировал закон инерции (1644). Высказал предположение, что атмосферное давление с увеличением высоты уменьшается. В 1637 году выходом в свет «Диоптрики», где содержались законы распространения света, отражения и преломления, идея эфира как переносчика света, объяснение радуги, положил начало оптике как науке. Первый математически вывел закон преломления света (независимо от В. Снеллиуса) на границе двух различных сред. Точная формулировка этого закона позволила усовершенствовать оптические приборы, которые тогда стали играть огромную роль в астрономии и навигации (а вскоре и в микроскопии). Дал теорию магнетизма. Вместе с конкретным научным открытием было совершено ещё одно, методологическое открытие. Обнаружилась необходимость и возможность постоянной (как это формулируется в Новое время-рефлективной) работы над собственным умом, необходимость и возможность постоянного обращения мысли на мысль, постоянного развития самой способности мыслить, открывать, изобретать. Рене Декарт также создал свою психологическую теорию, ориентируясь на объяснение принципов Галилея, новой механики Ньютона и открытие Гарвеем системы кровообращения. Крупнейшим открытиям Декарта, ставшим фундаментальным для последующей психологии, можно считать понятие о рефлексе и принцип рефлекторной деятельности. Схема рефлекса сводилась к следующему. Декарт представил модель организма как работающий механизм. При таком понимании живое тело не требует более вмешательства души; функции «машины тела», к которым относятся «восприятие, запечатление идей, удержание идей в памяти, внутренние стремления… совершаются в этой машине как движения часов». Наряду с учениями о механизмах тела разрабатывалась проблема аффектов (страстей) как телесных состояний, являющихся регуляторами психической жизни. Термин «страсть», или «аффект», в современной психологии указывает на определенные эмоциональные состояния.

Математические открытия

Находясь в коллегиальном колледже он доказал закон взаимности квадратичных вычетов. А в университете математик сумел построить правильный семнадцатиугольник с помощью линейки и циркуля и решил проблему построения правильных многоугольников. Этим достижением ученый дорожил больше всего. Настолько, что пожелал выгравировать на его посмертном памятнике круг, в котором бы находилась фигура с 17 углами.

В 1801 году Клаус издает труд «Арифметические исследования». Через 30 лет на свет появится очередной шедевр немецкого математика – «Теория биквадратичных вычетов». В нем приводятся доказательства важных арифметических теорем для вещественных и комплексных чисел.

Гаусс стал первым, кто представил доказательства основной теоремы алгебры и начал изучать внутреннюю геометрию поверхностей. Он также открыл кольцо целых комплексных гауссовых чисел, решил много математических проблем, вывел теорию сравнений, заложил основы римановой геометрии.

Философия Беркли

Еще будучи студентом, Беркли сделал для себя вывод, что естественные науки являются основополагающими. Своей целью он видел создание собственной, абсолютно новой философской системы, которая бы смогла остановить стремительный рост количества приверженцев материальных взглядов. С 1707 года Беркли вел дневник, в котором регулярно делал записи и пометки – именно так и создавалась его система философских взглядов.

Первым серьезным трудом Беркли стал анализ и критика сенсуалистического учения Локка. Отличительной чертой локковской и берклианской системы, исходившей из одних эмпирических предпосылок, были разные выводы. Отличался и тип самой системы – у Локка она была реалистической, у Беркли – идеалистической. Разным были взгляд на качества тех или иных предметов. Локк выделял первичные (длина, вес и т.д.) и вторичные, которые напрямую зависели от первых. Беркли же был твердо уверен – абсолютно все качества являются вторичными. Исходя из его суждений, первичные качества по Локку не могут быть объективными, ввиду их индивидуального восприятия каждым отдельным человеком. Так, в соответствии с берклианской философской системой, существование вторичных и первичных качеств обусловлено исключительно нашим восприятием.

Различными являются и представления о материи. Локк утверждал, что познается она путем абстракции, Беркли же был уверен, что это не возможно, как и понятие «абстрактной идеи» в общем. Здесь, так же как и с качествами предмета, конечный «результат» зависит от человека, воспринимающего материю – именно сознание рисует точное впечатление и образ, никакой общей идеи. Глядя на квадрат, считал Беркли, человек видит квадрат, а не какую-нибудь абстрактную форму. Исходя из его размышлений, абстрактная идея – не более чем обман слов.

Достижения в других научных сферах

Вице-гелиотроп. Латунь, золото, стекло, красное дерево (создан до 1801 года). С рукописной надписью: «Собственность господина Гаусса». Находится в Университете Гёттингена, первый Физический институт.

Настоящую известность Карлу Гауссу принесли вычисления, с помощью которых он определил положение планеты Цереры, открытой в 1801 году.

В последующем ученый не раз возвращается к астрономическим исследованиям. В 1811 году он рассчитывает орбиту новообнаруженной кометы, делает вычисления для определения расположения кометы «пожара Москвы» в 1812 году.

В 20-х годах 19 века Гаусс работает в сфере геодезии. Именно он создал новую науку – высшую геодезию. Также разрабатывает вычислительные методы для проведения геодезической съемки, издает цикл трудов по теории поверхностей, вошедших в публикацию «Исследования относительно кривых поверхностей» в 1822 году.

Обращается ученый и к физике. Он развивает теории капиллярности и системы линз, закладывает основы электромагнетизма. Совместно с Вильгельмом Вебером изобретает электрический телеграф.

Детство и юность

Джон Форбс Нэш-младший родился 13 июня 1928 г. в американском городе Блуфилд в Западной Виргинии.

Отец мальчика, Джон Форбс Нэш, работал инженером-электриком. Мать, Маргарет Вирджиния (в девичестве Мартин), была до замужества учительницей английского языка и латыни. В 1930 г. у Джона появилась младшая сестра Марта. Родители были протестантами, поэтому дети воспитывались в строгой религиозной атмосфере.

Джон посещал местный детский сад, а затем школу. Учился мальчик не слишком успешно, а из-за скучного преподавания математика будущему учёному совсем не нравилась.

Джон Форбс Нэш в детстве

Юный Нэш очень любил читать, и в возрасте 14 лет ему попалась книга Эрика Темпла Белла «Великие математики», которая произвела на мальчика неизгладимое впечатление. После прочтения книги Джон самостоятельно смог доказать малую теорему Ферма, чем очень удивил учителей. Ему была выделена стипендия для дальнейшего обучения.

Окончив школу, юноша поступил в Политехнический институт Карнеги. На тот момент он ещё не определился со специальностью. Сначала Джон пробовал изучать химию, потом – международную экономику, но вскоре понял, что хочет заниматься только математикой.

В молодости

Детство и ранние годы

Карл Фридрих Гаусс, сын бедняка и необразованной матери, самостоятельно разгадал загадку даты собственного рождения и определил её как 30 апреля 1777 г. Гаусс с детства проявлял все признаки гениальности. Главный труд всей своей жизни, «Арифметические исследования», юноша закончил ещё в 1798 г., когда ему был всего 21 год, хотя издан он будет лишь в 1801 г

Работа эта имела первостепенную важность для совершенствования теории чисел как научной дисциплины, и представила эту область знаний в том виде, в каком мы знаем её сегодня. Потрясающие способности Гаусса так поразили герцога Брауншвейгского, что он отправляет Карла на обучение в Карлов коллегиум (ныне – Брауншвейгский технический университет), который Гаусс посещает с 1792 г

по 1795 г. В 1795-1798 г.г. Гаусс переходит в Гёттингский университет. За свои университетские годы математик доказал немало значимых теорем.

Профессор в Корке

Дом на Гренвилл-плейс, 5 в Корке , в котором Буль жил между 1849 и 1855 годами и где он написал «Законы мысли» (фотография сделана во время ремонта).

Статус Буля как математика был признан после его назначения в 1849 году первым профессором математики Королевского колледжа в Корке (ныне Университетский колледж Корка (UCC)) в Ирландии. Он встретил свою будущую жену Мэри Эверест там в 1850 году, когда она навещала своего дядю Джона Райалла, профессора греческого языка. Они поженились несколько лет спустя в 1855 году. Он поддерживал связи с Линкольном, работая там с Э. Р. Ларкеном в кампании по сокращению проституции.

Интересные факты из жизни

Несколько любопытных фактов из биографии Евклида:

Самый древний известный математический трактат принадлежит Евклиду.
До сих пор нет данных о месте рождения и смерти великого ученого. Однако известно место занятий Евклида примерно 2400 лет назад и место его нахождения — Александрия. Интересно, что этот городок сегодня — второй по размерам в Египте после Каира;
Евклид смог создать 4 книжки по коническому виду сечений.
Фундаментальный труд «Начала» считается настолько важным для науки, что до сих пор его используют в жизни. Интересно, что есть другие публикации с подобным наименованием, но самый популярный — труд Евклида».
С самой юности Евклид обучался у именитого ученого Платона, обучавшего Аристотеля в Древней Греции. Сам же Платон обучался у Сократа.
По традиции геометрия сегодня носит название этого ученого.
Есть легенда, что когда один раз ученик величайшего математика спросил у него, как геометрия может помочь ему в жизни, то Евклид дал ему денег и прогнал с занятий.
Евклид до сих пор считается автором многочисленных книг, чье авторство не было подтверждено. Это разные труды, к примеру, публикации по музыке, философии и медицине. Официально известно, что великий ученый сделал открытие в оптических и астрономических областях.
Сегодня признают римановскую, лобачевскую и евклидову геометрию. Последняя — самая традиционная и часто используемая.
В первый раз евклидовский труд перевели в конце восемнадцатого века. При этом «Начала» впервые были переведены на армянский язык в одиннадцатом веке.
Любимая фраза: «Нет царского пути в геометрии».

В целом, Евклид является отцом геометрии, и он не случайно так называется. Он первым сделал сложное понятным и дал толчок развитию естественных наук. Его книги неоценимы по значимости и применяются сегодня в области математических и геометрических наук во всем мире.

Личная жизнь

Но если в мире научных открытий у известного учёного всё складывалось замечательно, то о его семейной жизни информации очень мало. Скорее всего, жены у него не было. А по воспоминаниям современников Рене был молчаливым человеком, иногда мог вести себя очень высокомерно. Не любил он большие и шумные компании, предпочитая небольшой круг близких друзей. Но рядом с ними он был общителен, любезен и активен.

Так, уже в зрелые годы он был влюблён в свою служанку, которая впоследствии родила ему дочь. Декарт очень любил девочку, хотя она и считалась незаконнорождённой. Но когда Франсине исполнилось пять лет, она заболела скарлатиной и умерла. Это стало самой большой трагедией в его жизни.

Российские математики

Не меньший вклад в науку сделали российские математики. Многие открытия лучших умов России получили известность далеко за пределами страны. Самые серьезные достижения русской математической науки пришлись на вторую половину 19 века.

Николай Лобачевский

Одаренный русский ученый, сумевший открыть отдельное направление в геометрии, получившее название «неэвклидовой» или геометрии Лобачевского.

Ему удалось получить положительные результаты в решении тонких теорем о тригонометрических рядах, определить признаки сходимости рядов.

Публикации ученого в области алгебры, физики, астрономии широко получили признание в научном мире.

Софья Ковалевская

Является первой в России женщиной, получившей звание профессора математики. Основной сферой исследования Ковалевской была небесная механика и математическая физика.

Талантливой женщине-ученому удалось найти третий вариант решения задачи о вращении тел вокруг неподвижной точки. Софья Васильевна занималась поиском решения задачи Лапласа о равновесии колец Сатурна. Решила одну из задач Коши. В 1889 году Ковалевская была награждена престижной премией Парижской академии за изучение вращения тяжелого несимметричного волчка.

Андрей Колмогоров

Знаменитый русский ученый, сделавший весомый вклад в разработку современной теории вероятности. Работы исследователя, применяющие научный подход к художественной литературе, известны на весь мир.

Колмогоров является первым русским ученым-кибернетиком. Ему принадлежит множество значимых открытий в геометрии, математической логике, теории меры и других областях математики.

«Рассуждение о методе»

Декарт Рене (краткая биография является тому подтверждением) имел философскую точку зрения, которая иллюстрировала попытки европейской культуры и традиций освободиться от старых понятий и построить новую жизнь, а также и науку. Истиной, по рассуждению ученого, считается только «естественный свет» человеческого разума.

Конечно, Декарт не исключает ценность человеческого опыта, но он считает, что единственная его функция – это помощь разуму в тех случаях, в которых сил для познания недостаточно.

Рене Декарт, идеи которого используются в современной философии, рассмотрел понятие дедукции, или «движения мысли», в котором соединяются интуитивные истины. Человеческий интеллект слаб, поэтому нуждается в постоянной проверке сделанных шагов. Эта методика нужна для того, чтобы проверить отсутствие пробелов в рассуждениях. Такую проверку ученый называет индукцией. А вот итог дедукции – это система всеобщего знания, или «универсальной науки». Такую науку Рене сравнивает с деревом. Его корень – это метафизика, ствол – физика, а ветви составляют такие науки, как механика, этика и медицина. Каждая из этих наук должна приносить пользу. Для того чтобы каждая отрасль была максимально эффективной, абсолютно правильной должна быть метафизика.

Биография Леонарда Эйлера (1707-1783 гг.)

Краткая биография:

Имя: Леонард Эйлер

Дата рождения: 15 апреля 1707 г.

Дата смерти: 7 сентября 1783 г.

Образование: Базельский университет

Место рождения: Базель, Швейцария

Место смерти: Санкт-Петербург, Российская империя

Леонард Эйлер – математик и механик: биография с фото, открытия и вклад в науку, исследование движения света сквозь среду, сотрудничество с Лагранжем, работы.

Леонард Эйлер родился в Швейцарии, в Базеле. Поступил и окончил там гимназию, в Базельском университете посещал и слушал лекции И. Бернулли. Степень магистра была получена уже в 1723 году. В 1726 году получил приглашение от Академии Наук в Петербурге, отправился в Россию, где стал адъюнктом в области математики.

Обосновался на кафедре физики в 1730 году, и уже в 1733 — стал академиком. Находясь в России 15 лет, смог написать за это время самый первый учебник в мире по теоретической механике и другие работы.

В 1741 году прусский король Фридрих II пригласил Эйлера в Берлин, и ученый принял приглашение. Но, даже находясь там, связь с Петербургом оставалась. Написал статьи, посвященные баллистике, и выпустил три тома со своими статьями в 1746 году. Уже в 1749 году был опубликован труд в двух томах, который посвящен вопросам, связанным с навигацией в математической форме. Сделал множество разнообразных открытий в области математического анализа, позже, все открытия были собраны в книге «Введение в анализ бесконечно малых величин», которая была опубликована в 1748 году. Немного погодя создал и опубликовал трактат (4 тома). Первый том рассказывает о дифференциальном исчислении, вышел в 1755 году, в Берлине. Второй, третий и четвертый тома посвящены интегральному исчислению, опубликованы уже в Петербурге, в 1768-1770 годах. Однако, стоит отметить, что четвертый том разбирает вариационное исчисление, которое было создано Эйлером и Лагранжем. Одновременно с этим, Эйлер занимался вопросом о прохождении света через многочисленные среды, а также эффект хроматизма. В 1747 году им был продуман и предложен сложный объектив.

Возвращение в Россию состоялось в 1766 году. Эйлер ослеп, и в связи с этим свою новую работу ему пришлось надиктовывать. Эта работа, «Элементы алгебры», вышла в свет уже в 1768 году. Тогда же печатались и другие его работы, в том числе три тома из трактата, описываемого выше.

Академия Наук в Париже в 1755 году провозгласила Эйлера девятым присоединенным членом (несмотря на то, что их всего восемь). С данным решением французское правительство было не согласно.

Эйлер рассматривал многочисленные вопросы, несмотря на их трудность и прочее. Создал более 865 работ и исследований. Оказал большое воздействие на развитие Российского математического просвещения в XVIII веке. Математическая школа в Петербурге, в составе которой были разнообразные академики, вместе с Эйлером осуществили немалую работу относительно просвещения, создали необходимую для обучения литературу, ряд увлекательных исследований.

Умер в Петербурге, в 1783 году.

Континентальные взгляды в философии

В разрезе своего представления о существующем вокруг мире, Джордж Беркли в результате долгой исследовательской работы, выдвинул немало интересных суждений. Одно из них звучит примерно так: Бог – единственная сила, способствующая зарождению в человеческой душе какого-либо чувства. Все что человек видит и слышит, открывая глаза, не зависит от его желания, и он не способен выбирать между «видением» и «не видением». Следовательно, есть другая, сила, которая и производит в душе человека все ощущения.

Труды Беркли детально изучаются по сегодняшний день, а некоторым исследователям удается выдвинуть довольно нестандартные теории. Так, бытует мнение (не подтвержденное, но имеющее прав на существование), что философские взгляды Беркли формировались на основании теории Мальбранша. Если верить данному суждению, выходит, что взгляды Джорджа Беркли очень схожи со взглядами представителей картезианской философской школы, в то время как эмпиризм в его учениях отсутствует.

Книги II—XIII

II книга — теоремы так называемой «геометрической алгебры».

III книга — предложения об окружностях, их касательных и хордах, центральных и вписанных углах.

IV книга — предложения о вписанных и описанных многоугольниках, о построении правильных многоугольников.

V книга — общая теория отношений, разработанная Евдоксом Книдским.

VI книга — учение о подобии геометрических фигур. Эта книга завершает евклидову планиметрию.

VII, VIII и IX книги посвящены теоретической арифметике. Евклид в качестве чисел рассматривает исключительно натуральные числа; для него «Число есть совокупность единиц». Здесь излагаются теория делимости и пропорций, доказывается бесконечность множества простых чисел, приводится алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, строятся чётные совершенные числа. Евклид доказывает также формулу для суммы геометрической прогрессии.

X книга — классификация несоизмеримых величин. Это самая объёмная из книг «Начал».

XI книга — начала стереометрии: теоремы о взаимном расположении прямых и плоскостей; теоремы о телесных углах, объём параллелепипеда и призмы, теоремы о равенстве и подобии параллелепипедов.

XII книга — теоремы о пирамидах и конусах, доказываемые с помощью метода исчерпывания. Здесь доказывается, например, теорема о том, что объём конуса составляет одну треть от объёма цилиндра с теми же основанием и высотой.

XIII книга — построение правильных многогранников; доказательство того, что существует ровно пять правильных многогранников.

Евклид нигде в книге не ссылается на других греческих математиков, хотя несомненно опирается на их результаты. Историки науки показали, что прототипом для труда Евклида послужили более ранние сочинения античных математиков:

Книги I—IV и XI — «Начала» Гиппократа Хиосского.
Книги V—VI и XII — труды Евдокса Книдского.
Книги VII—IX — сочинения Архита Тарентского и других пифагорейцев. По мнению Ван дер Вардена, это самая древняя по содержанию часть «Начал», восходящая к V веку до н. э.
Книги X и XIII — труды Теэтета Афинского.

Вопрос о том, содержат ли «Начала» какие-либо результаты самого Евклида или автор занимался только систематизацией и унификацией накопленных знаний, является предметом дискуссий. Есть предположение, что алгоритм построения правильного 15-угольника разработан Евклидом; вероятно, он же произвёл отбор и окончательную формулировку аксиом и постулатов.

В целом содержание «Начал» покрывает значительную часть античной теоретической математики. Однако некоторая часть известного древнегреческим математикам материала осталась вне этого труда — например, конические сечения (Евклид посвятил им отдельный труд, который не сохранился), длина окружности, теория приближённых вычислений.

Карьера

Буль работал помощником учителя в Донкастере, а также недолгое время преподавал в Ливерпуле. Некоторое время он был связан с открывшимся в 1833 году институтом механики Линкольна. А в 1834 году он открыл свою школу в Линкольне.

В течение этого времени он много времени уделял социальной работе и образованию взрослых. Он основал «Приют раскаявшихся женщин», целью которого была реабилитация проституток. С целью образования неимущих, Буль также работал в институте механики. Через четыре года Буль стал владельцем «Hall’s Academy» в Уоддингтоне, под Линкольном. В 1839 году он представил несколько работ, среди которых были «Теория математических преобразований» для «Кембриджского математического журнала».

В этих работах речь шла о дифференциальных уравнениях и алгебраической проблеме линейной трансформации путём выделения идеи инвариантной линейной трансформации через выделение идеи инвариантности.

В 1840 году он вернулся в Линкольн для руководства закрытой школой.

В 1841 году он открыл теорию инвариантов – новый раздел математики. Этот раздел математики впоследствии был источником вдохновения Эйнштейна.

В 1844 году он анализировал комбинированные методы алгебры и исчислений в публикации с названием «Философские труды королевского общества».

В 1847 году, совместно с Э. Р. Ларкеном, он основал жилищно-строительное общество. В том же году в памфлете «Математический анализ логики» он высказал мнение, что логика должна быть связана с математикой.

Инновационный вклад Буля в математику был по-настоящему эффективен при создании цифрового компьютера и электронных схем.

В 1849 году он стал первым профессором математики в Королевском колледже в Корке, Ирландия.

В 1854 году он занимался алгеброй и логикой, и его труды в этой области более известны как булева алгебра (алгебра логики). В том же году он ввёл понятие символический метод логического вывода в публикации «Законы мысли».

Булева алгебра служит в качестве основ анализа обоснованности логических суждений, так как она носит бинарный характер утверждений, которые могут оказаться либо положительными, либо ложными.

Метод бинарности и логические элементы булевой логики используются в телефонной коммутации и в электронных компьютерах во время их создания и работы.

Во второй части «Закона мысли» Буль пытался открыть общий метод в вычислении вероятностей.

В 1857 году Буль представил публикацию «О сравнении трансцендентных функций» с определёнными наложениями на теорию определённых интегралов. В публикации он изучает сумму остатков рациональной функции. А частью изучения стало доказательство булева тождества.

В 1859 году Буль публикует «Трактат по дифференциальным уравнениям», в котором он сообщает об общем символическом методе, в 1860 году он публикует продолжение с названием «Трактат об исчислении конечных разностей».

Буль внёс вклад в такие науки как: электроника, математика, теория информации, логика, кибернетика и информатика.

Интересные факты из жизни

Несколько любопытных фактов из биографии Евклида:

Самый древний известный математический трактат принадлежит Евклиду.
До сих пор нет данных о месте рождения и смерти великого ученого. Однако известно место занятий Евклида примерно 2400 лет назад и место его нахождения Александрия. Интересно, что этот городок сегодня второй по размерам в Египте после Каира,
Евклид смог создать 4 книжки по коническому виду сечений.
Фундаментальный труд «Начала» считается настолько важным для науки, что до сих пор его используют в жизни. Интересно, что есть другие публикации с подобным наименованием, но самый популярный труд Евклида».
С самой юности Евклид обучался у именитого ученого Платона, обучавшего Аристотеля в Древней Греции. Сам же Платон обучался у Сократа.
По традиции геометрия сегодня носит название этого ученого.
Есть легенда, что когда один раз ученик величайшего математика спросил у него, как геометрия может помочь ему в жизни, то Евклид дал ему денег и прогнал с занятий.
Евклид до сих пор считается автором многочисленных книг, чье авторство не было подтверждено. Это разные труды, к примеру, публикации по музыке, философии и медицине. Официально известно, что великий ученый сделал открытие в оптических и астрономических областях.
Сегодня признают римановскую, лобачевскую и евклидову геометрию. Последняя самая традиционная и часто используемая.
В первый раз евклидовский труд перевели в конце восемнадцатого века. При этом «Начала» впервые были переведены на армянский язык в одиннадцатом веке.
Любимая фраза: «Нет царского пути в геометрии».

Рене Декарт: достижения в области физики и математики

Ученый являлся первым, кто ввел коэффициенты, переменные величины, а также обозначения степеней. Внес свой вклад в теорию уравнений: сформулировал правило знаков для нахождения числа отрицательных и положительных корней. Также показал, что уравнение третьей степени можно решить в квадратных радикалах или же с помощью линейки и циркуля.

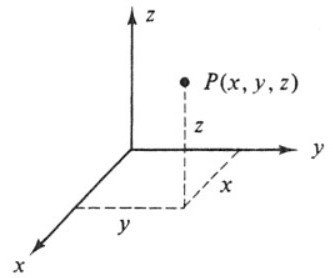
Вместе с Пьером Ферма стал автором аналитической геометрии. Данная наука позволила алгебраизировать геометрию и рассматривать ее с помощью координатного метода. Предложенная им координатная система названа в честь ученого.

В 1637 году Декарт написал пособие «Геометрия», в котором и рассказал о взаимодействии алгебры и геометрии. Здесь впервые рассматривались такие понятия, как функция и переменное значение.

Также в эту работу были включены линии, которые описывают при своем движении шарнирные механизмы. Исследуя линзы, ученый изложил основные методы построения касательных и нормалей к плоским кривым.

В настоящее время всему миру известно, что открыл Рене Декарт. Его работа «Геометрия» повлияла на развитие всех направлений математических наук. Благодаря изобретенной им системе координат, получилось реально истолковать происхождение отрицательного числа.

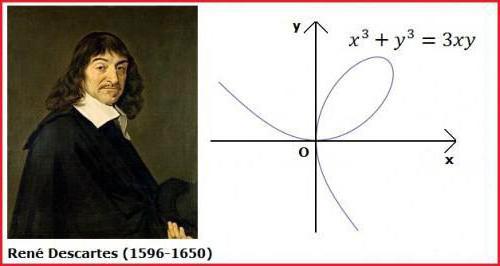
Работы Декарта также имеют большое значение и для физики. Смог сформулировать закон инерции, а также стал автором закона о преломлении световых лучей.

«Начала» Евклида

Главный труд Евклида – «Начала» (или «Элементы», в оригинале «Стойхейа»). «Начала» Евклида состоят из 13 книг. Позднее к ним были прибавлены еще две книги.

Первые шесть книг «Начал» посвящены геометрии на плоскости – планиметрии. В философско-теоретическом отношении, в плане философии математики особенно интересна первая книга, которая начинается с определений, постулатов и аксиом, учение о которых было заложено Аристотелем.

Евклид определяет точку как то, что не имеет частей. Линия – длина без ширины. Концы линии – точки. Прямая линия равно расположена по отношению к точкам на ней. Поверхность есть то, что имеет только длину и ширину. Концы поверхности – линии. Плоская поверхность есть та, которая равно расположена по отношению к прямым на ней. И так далее. Таковы определения Евклида.

Статуя Евклида в музее Оксфордского университета

Далее следуют постулаты, т. е. то, что допускается. Допустим, что от всякой точки до всякой точки можно провести прямую линию, что ограниченную прямую можно непрерывно продолжить по прямой, что из любой точки, принятой за центр, можно всяким раствором циркуля описать круг, что все прямые углы равны между собой и что если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то, будучи продолженными, эти две прямые рано или поздно встретятся с той стороны, где углы меньше двух прямых.

Аксиомы Евклида говорят о том, что величины, равные третьей величине, равны между собой, что если к равным прибавить равные, то и целые будут равными, и т. д.

Далее, в первой же книге «Начал» Евклида, рассматриваются треугольники, параллельные линии, параллелограммы. Вторая книга «Начал» содержит геометрическую алгебру: числа и отношения чисел выражаются в пространственных величинах и в их пространственных же отношениях. Третья книга «Начал» исследует геометрию круга и окружности, четвертая – многоугольники. Пятая книга дает теорию пропорций как для соизмеримых, так и для несоизмеримых величин. В книге VI Евклид прилагает эти теории к планиметрии. Книги VII – X содержат теорию чисел, причем X книга трактует иррациональные линии. XI, XII и XIII книги «Начал» посвящены стереометрии, при этом в XII книге применяется метод исчерпания.

В строгом смысле слова Евклида нельзя считать «отцом геометрии». Свои «Начала» были у Гиппократа Хиосского в V в. до н. э. В IV в. до н. э. «Начала» были у Леона, и у Феудия Магнесийского. Метод исчерпания применял Евдокс Книдский, возможный учитель Евклида по Академии. Проблемой иррациональности занимались пифагореец Гиппас Метапонтский, Феодор Киренский, Теэтет Афинский… Однако Евклид – не простой передатчик сделанного до него математиками. В «Началах» Евклида мы видим завершение математики как стройной науки, исходящей из определений, постулатов и аксиом и построенной дедуктивно. Математика Евклида – вершина древнегреческой дедуктивной науки. Она резко отличается от ближневосточной математики с ее практической приблизительной рецептурностью. Не случайно «Начала» Евклида по их логической стройности, ясности, изяществу и законченности сравнивают с .

Правда, существовала легенда, что сам Евклид – не единственный автор дошедших до нас «Начал», что он сам дал лишь догматическое изложение материала, без доказательств, что доказательства были добавлены вышеупомянутым Теоном Александрийским. Теон Александрийский действительно занимался проблематикой «Начал». Но не он один. Этим же занимались и Прокл, и Симплиций. «Начала» Евклида были частично переведены на латинский язык Цензорином и Боэцием. Но эти их переводы затерялись. На Западе вплоть до конца XII в. находились в обращении тезисы Евклида без доказательств.

Что касается Ближнего Востока, то там Евклид был известен в переводах с греческого на сирийский, а с сирийского – на арабский. Первым арабским философом, который заинтересовался Евклидом, был, по-видимому, аль-Кинди (IX в.). Его интерес ограничивался евклидовой «Оптикой». Однако затем последовала масса переводов и комментариев на «Начала». Эти арабские тексты были переведены в XIII в. на латинский язык. Первый латинский перевод с греческого оригинала был делан в Европе в 1493 г. и отпечатан в 1505 г. в Венеции. Но до 1572 г., когда Федерико Коммандино в своем латинском переводе исправил эту ошибку, Евклида-математика путали с Евклидом Мегариком.

Готфрид Вильгельм Лейбниц

Этот известный математик жил в одно время с Исааком Ньютоном, поэтому многие его открытия находились в своеобразной тени из-за всемирной славы гениального оппонента.

Тем не менее, вклад Лейбница в науку не менее значителен. Например, в алгебре и сегодня применяются его обозначения бесконечно малых величин.

Немецкий ученый поспособствовал появлению первых цифровых калькуляторов, доработав двоичную систему исчисления. Ряд работ исследователя посвящена биномиальным коэффициентам и арифметическим рядам. Также им был разработан универсальный алгоритм для определения признаков делимости чисел.

Джордж Буль: биография (кратко)

Этот ученый появился на свет 2 ноября 1815 года в небогатой рабочей семье. Местом его рождения был город Линкольн, располагающийся на востоке Англии. Его отец Джон изготавливал обувь, а мать Мэри до той поры, пока не вышла замуж, была камеристкой. Отец Джорджа серьезно увлекался наукой и уделял недостаточно времени своему основному делу. В семье долго не было детей, но когда супруги уже утратили всякую надежду, у них появился долгожданный сын.

Джордж Буль появился на свет очень слабым, но ему суждено было выжить, окрепнуть и стать настоящим гением.

В неполные два года он стал ходить в школу, предназначенную для детей торговцев. После до семи лет мальчик посещал занятия в коммерческой школе, руководил данным учебным заведением друг его отца.