Ряды динамики в статистике - характеристика и применение, средний уровень интервального ряда динамики

Средние значения показателей рядов динамики

Средние значения показателей рядов динамики выражают уровни и типичные значения их изменений
в определённый период времени. Прежде чем рассматривать средние значения показателей рядов динамики, разграничим
понятия интервальных и моментных рядов динамики.

Интервальные ряды динамики характеризуют значения изучаемого явления за некоторый
период времени, например, за месяц, за год, за пять лет. Моментные ряды динамики характеризуют значения
изучаемого явления в какой-то определённый момент времени, например, на начало или конец месяца, начало
или конец года и так далее. В предыдущем параграфе мы рассматривали интервальный ряд динамики и его
показатели.

Средний уровень интервального ряда динамики вычисляется путём деления суммы уровней
ряда на число уровней:

Пример 5. Вычислить среднегодовой объём экспорта предприятия «Х».

Решение. Вычислим средний уровень по формуле для интервального ряда динамики:

Средний уровень моментного ряда динамики, если между моментами — равные
промежутки времени, вычисляется по формуле средней хронологической:

Пример 6. Вычислить среднее число сотрудников предприятия «Х» на
начало года. В таблице ниже даны значения числа сотрудников на начало каждого года с 2013 по 2017 годы.

Момент	Число
1 янв. 2013	1113
1 янв. 2014	1122
1 янв. 2015	1110
1 янв. 2016	1130
1 янв. 2017	1222

Решение. Вычисляем по формуле хронологической средней:

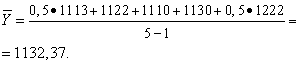
Если между моментами ряда динамики — не равные промежутки времени, средний уровень
моментного ряда вычисляется по формуле средней хронологической взвешенной:

В этой формуле
— — уровни ряда динамики,
— — периоды
времени, например, 1 месяц, 2 месяца, 1 год, 2 года, 3 года… Все периоды времени должны выражаться в одной
и той же единице измерения (днях, месяцах, годах и др.).

Средний абсолютный прирост (снижение) выражает абсолютную величину, на которую в
среднем в каждую единицу времени в соответствующий период выросли или снизились показатели исследуемого
явления. Его вычисляют путём деления суммы цепных абсолютных приростов на число абсолютных приростов:

где —
число абсолютных приростов.

Если нет данных о цепных абсолютных приростах, но известны начальный и конечный уровни
ряда динамики, то средний абсолютный прирост можно вычислить через базовый абсолютный прирост по формуле

Пример 7. Используя данные об экспорте предприятия «Х», вычислить
среднегодовой прирост экспорта.

Решение. Вычислим интересующий нас показатель через сумму цепных абсолютных приростов:

Вычислим его же через базовый абсолютный прирост:

Как видим, получили один и тот же результат.

Средний темп роста является показателем изменения интенсивности изменения уровней ряда
динамики. Он характеризует среднюю интенсивность развития исследуемого явления, показывая, во сколько раз
в среднем в единицу времени изменились уровни ряда динамики. Средний темп роста можно выразить в
коэффициентах или процентах.

Цепной средний темп роста вычисляется по формуле среднего геометрического:

где n — число цепных темпов роста,

T — индивидуальные цепные темпы роста, выраженные в коэффициентах.

Если нет информации о каждом цепном темпе роста, средний темп роста можно вычислить
по формуле с использованием последнего и первого уровней ряда динамики

Пример 8. Вычислить средний темп роста экспорта предприятия «Х».

Решение. Вычисляем по формуле среднего геометрического:

Вычисляем по формуле с использованием последнего и первого уровней ряда динамики:

Получили один и тот же результат.

Средний темп прироста показывает, на сколько процентов в среднем увеличился (если
он со знаком «плюс») или уменьшился (если со знаком «минус») уровень исследуемого явления в течение
всего рассматриваемого периода. Средний темп прироста вычисляется путём вычитания из среднего темпа
роста 100% (если он выражен в процентах) или единицы (если он выражен в виде коэффициента).

В нашем примере:

Виды рядов динамики в статистике

Разделяют последовательности по временным показателям и по представлению чисел:

Отсечка производится по конкретному отрезку времени (моментный ряд) или суммируется за какой-то промежуток (интервальный ряд). В приведенном примере – первый случай. Показано состояние на определенную дату. Попытка что-то просуммировать даст бессмысленное число. Второй способ актуален, если, например, характеризуется выпуск товаров за неделю, месяц, квартал.
С постоянным или изменяющимся временным отрезком. В нашем случае отображаются регулярные годовые замеры.
Показаны абсолютные, средние или относительные безразмерные числа. У нас иллюстрируется количество живущих в государстве людей без каких-либо алгебраических вмешательств.
По сути показателей. Может сопоставляться курс валюты (одномерный критерий), а может состоять из объемов закупки разных валют (многомерный). В примере фигурирует только одна величина.

Показатели анализа рядов динамики

Методы анализа сводятся к видоизменению полученных данных к виду, облегчающему отслеживание динамики и выявляющему ее направленность. Так или иначе придется сопоставлять уровни для понимания темпов роста / убыли.

Для оценки применяются абсолютные (вычитание уровней) и относительные (отношение уровней ряда) величины.

Базисные показатели можно получить, если сравнивать с первым элементом. Цепные показатели – с соседними.

Это базисная и цепная абсолютные разницы соответственно.

То же в относительном выражении. В таком виде мы получим характеристику в виде коэффициента. Для более наглядного представления следует умножить на «100» и получить %%.

Надо заметить, что цепные критерии имеют свойства накапливаться и переходить в базисные:

И самые важные для оценки параметров динамики понятия — темпы:

Опять же в абсолютном и относительных видах. Если речь идет об анализе плавной кривой, то отношение заменит производная, указывающая на тангенс угла наклона касательной прямой.

Об усредненных величинах мы уже говорили. Стоит немного вернуться и рассмотреть их в связи с темпами:

Так выглядят базисный и цепной средние темпы прироста:

А вот так в относительных единицах.

Теперь на основании изложенного дополним нашу исходную таблицу и сделаем напрашивающиеся выводы.

Вполне очевидно, что отрицательные значения абсолютных величин и менее 1 относительные указывают на падение населения. При этом темпы роста ниже 0, и это указывает на сохранение неблагоприятной тенденции.

Задача — Ряды динамики с решением

Теория по решению задач.

Рядом динамики называется ряд статистических чисел, которые характеризуют изменение величины общественного явление во времени.

Моментный ряд динамики – это ряд динами, уровни которого характеризуют размеры общественно-экономических явлений по состоянию на определенный момент.

В моментных рядах динамики средние уровни вычисляются двумя способами:

1) если ряд динамики имеет равные промежутки времени между двумя составными датами:

, где

— средний уровень ряда динамики;

у – абсолютные уровни ряда динами;

n – число абсолютных уровней ряда динамики.

2) если ряд динамики имеет неодинаковые промежутки времени между двумя составными датами:

, где

t – периоды времени между датами.

Периодический (интервальный) ряд – это ряд динамики, уровни которого характеризуют размеры общественно-экономических явлений за определенные периоды времени (неделя, месяц, полугодие и т. д.).

Средние уровни в периодических рядах исчисляются как простая средняя арифметическая:

Один из важнейших вопросов, возникающих при изучении рядов динамики – это выявление тенденции развития экономического явления в динамике. Для этой цели применяются разнообразные статистические методы, в частности:

— метод укрупнения периодов:

у1=у1+у2+у3

у2=у4+у5+у6

у3=у7+у8+у9 и т. д.

— метод скользящей средней:

и т. д.

— метод аналитического выравнивания:

, где

t – время

n – число членов ряда

у – исходные уровни ряда динамики

а0 и а1 – параметры уравнения, которые необходимо определять.

Основные показатели рядов динамики:

1. Абсолютный прирост (∆у):

а) базисный ∆уб=уn-уо

б) цепной ∆уц=уn-уn-1

∆уб – абсолютный прирост базисный;

∆уц – абсолютный прирост цепной;

уn — уровень сравниваемый;

у0 – уровень периода, принятого за базу сравнение;

уn-1 – уровень, предшествующий сравниваемому периоду.

2. Средний абсолютный прирост ():

n – число показателей в периоде.

3. Абсолютное значение одного процента прироста (А):

∆Т – темп прироста

4. Темп роста (Т):

— базисный

— цепной

5. Темп прироста (∆Т):

— базисный:

— цепной:

6. Средний темп роста ()

у1, у2, уn –коэффициенты цепного темпа роста

n – число коэффициентов

уо и уn – начальный и конечный абсолютные показатели ряда динамики.

7. средний темп прироста (

Задача по товарообороту

Имеется следующая информация о реализации продуктов сельскохозяйственного производства магазинами города:

Среднегодовая реализация, (тыс. грн.):

Таблица № 1

Квартал	1998г.	1999г.	2000г.
1	340	515	435
2	280	330	420
3	420	438	380
4	510	240	377

Для выявления основной тенденции развития товарооборота произведите сглаживание уровней ряда динамики:

1. Методом укрепления периодов по трем кварталам.

2. Методом скользящей средней.

Ход решения задачи:

1. Метод укрупнения периодов:

у1=у1+у2+у3 у1=340+280+420=1040

у2=у4+у5+у6 у2=510+515 +320=1355

у3=у7+у8+у9 у3=438+240+435=1113

у4=у10+у11+у12 у4=420+380+377=1177

Таким образом, укрупненный ряд динамики имеет следующий вид:

1040; 1355; 1113; 1177.

2. Метод скользящей средней:

Т. о. выровненный ряд динамики примет следующий вид:

346,7; 403,3; 481,7; 451,7; 427,7; 336; 371; 365; 411,7; 292,3.

Задача по приростам

Имеется следующая информация о выпуске продукции заводом за 1996-2001 г. г. (тыс. грн.).

Таблица № 2

Годы	1996г.	1997г.	1998г.	1999г.	2000г.	2001г.
Валовая продукция	30,2	33,4	28,6	29,4	35,8	31,7

Определите:

1) абсолютные приросты;

2) темп роста и прироста;

3) абсолютное значение 1 % прироста;

4) средний абсолютный прирост;

5) среднегодовой темп роста и прироста.

Ход решения задачи:

1. Абсолютные приросты:

∆уб=уn-уо ∆уц=уn-уn-1

97г.: 33,4-30,2=3,2 33,4-30,2=3,2

98г.: 28,6-30,2=-1,6 28,6-33.ю4=-4,8

99г.: 29,4-30,2=-0,8 29,4-28,6=0,8

00г.: 35,8-30,2=5.6 35,8-29,4=6,4

01г.: 31,7-30,2=1,56 31,7-35,8=-4,1

2. Темпы роста и прироста:

а) темпы роста:

б) темпы прироста:

или вторым способом:

∆Тб=Тб-1 (или 100 %)

∆Тц=Тц-1 (или 100 %)

97г.: 1,106-1=0,106 (10,6%) 1,106-1=0,106 (10,6%)

98г.: 0,947-1=-0,053 (-5,3%) 0,856-1=-0,144 (-14,4%)

99г.: 0,973-1=-0,027 (-2,7%) 1,028-1=0,028 (2,8%)

00г.: 1,185-1=0,185 (18,5%) 1,218-1=0,218 (21,8%)

01г.: 1,05-1=0,05 (5%) 0,885-1=-0,115 (-11,5%)

3. Определяем абсолютное значение 1 % прироста

97г.: 0,01х30,2=0,302

98г.: 0,01х33,4=0,334

99г.: 0,01х28.6=0,286

00г.: 0,01х29,4=0,294

01г.: 0,01х35,8=0,358

4. Определим средний абсолютный прирост:

или вторым способом:

5. Определим среднегодовой темп роста и прироста:

а) среднегодовой темп роста

вторым способом

б) среднегодовой темп прироста:

Другие статьи по данной теме:

назад: Выборочное наблюдение: понятие, виды, ошибки выборки,
оценка результатов
далее: Экономические индексы в статистике: понятие, виды, формулы. Примеры решения
задач

Список использованных источников

Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями.
Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики,
информатики, финансов и права. — М., 2003;
Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика»
для студентов экономических специальностей: УрГЭУ, 2007;

Методы выравнивания рядов динамики

Выравнивание используется для определения общего направления динамики процессов. Кратковременные случайные всплески роста / падения иногда нарушают целостность восприятия картины.

Ещё можно заметить, что:

Увеличение периодов позволяет построить данные таким образом, чтобы изменения явно демонстрировали основную линию. Выравниваются средние значения.
Плавающая средняя означает, что она подсчитывается из определенного числа соседних уровней. По новым правилам построения организуется новый ряд из средних. Метод оптимален, если графическая интерпретация близка к прямой. В противном случае искажение динамики может оказаться чрезмерным.
Аналитический метод сводится к аппроксимации параметров математическим уравнением с высокой корреляцией. Дальнейшая работа базируется на нем. Так легче выявить тенденцию, можно позволить какие-то прогнозы. Облегчается использование численных методов.

Расчеты среднего уровня в рядах динамики

Существуют случаи, когда требуются какие-то резюмирующие значения. Среднее – из таких. При этом методики его определения для разных видов рядов отличаются.

Интервальный ряд динамики

В этом случае требуется просто поиск среднего арифметического. Таким образом можно показать какие-то сезонные колебания производства, продаж.

Рассчитать можно по формуле:

где Y – уровни;

n – их количество.

В нашем случае подобная цифирь полезной нагрузки не несет, только для наглядности:

(144,2 + … + 141,9) / 6 = 866,6 / 6 = 142,77.

Таково среднее население за 5 лет.

Моментный ряд динамики

Если разрыв в датах неизменен, то можно записать последовательность в средних значениях. Получим (n – 1) чисел такого вида

После нехитрых выкладок обнаруживаем, что

y(1), y(n) – базисный и конечный уровни;

y(i) – внутренние.

Считаем:

((141.2 + 141,9) / 2 + 143,5 + … + 142) / 5 = (143,05 + 570,5) / 2 = 142,71.

Мы получили среднее хронологическое.

Но это для равных отрезков. Когда они меняются, необходимо учитывать временной фактор. Если уровни меняются с течением времени, то выводится такое:

Выражение несколько упрощается, если уровни постоянны до следующей отсечки.

t(i) – длительность периода, когда уровень i зафиксирован.

Виды рядов динамики

Объединение радов происходит по:

Времени. Это моментные и интервальные ряды.
Форме представления. К ним относятся абсолютные, относительные и средние величины.
Интервалам времени. Подразделяются на равномерные и неравномерные ряды.
Числу смысловых статистических величин. Это изолированные и комплексные ряды.

Чтобы без ошибок построить динамические ряды, необходимо сопоставлять уровни рядов разных периодов. Для этого у них должны быть однородные величины. Также ряды предполагают охват явления с одинаковой полнотой.

Не допускать погрешностей в анализе динамики помогает смыкание рядов динамики. Суть понятия в проведении подготовительной работы до основных расчетов. Во время подготовки ряды объединяются в один. Уровни этих рядов рассчитаны по разным методологиям. Смыкание также включает преобразования, при которых абсолютные уровни рядов приводятся к общему основанию. Это действие помогает избежать несопоставимости уровней.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Примеры решения задач по теме «Ряды динамики в статистике»

Задача 1. Данные о площадях под картофелем до и после изменения границ района,
тысяч гектаров:

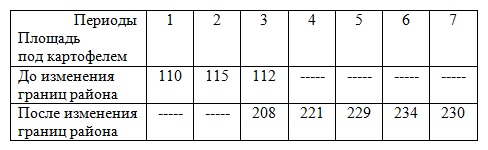Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района.

Решение

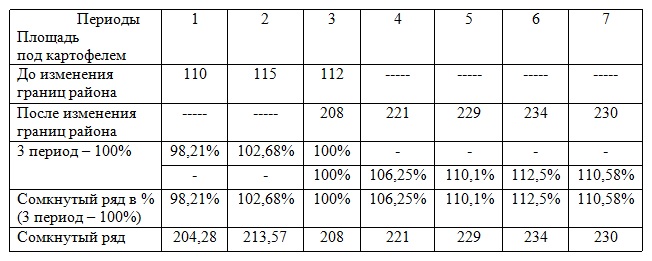Примем за базу сравнения третий период – период, за который есть данные как в прежних, так и в старых
границах района. Затем эти два ряда с одинаковой базой смыкаем в один.

Задача 2. Имеется информация об экспорте продукции из региона за ряд лет:

Определить: 1) цепные и базисные: а) абсолютные приросты; б) темпы роста; в) темпы прироста; 2)абсолютное содержание одного
процента прироста; 3) средние показатели: а) средний уровень ряда; б) среднегодовой абсолютный прирост; в)
среднегодовой темп роста; г) среднегодовой темп прироста.

Решение

Напомним, что:
— если каждый текущий уровень сравнивать с предыдущим, то мы получим цепные показатели;
— если каждый текущий уровень сравнивать с первоначальным, то получим базисные показатели.

Для решения расширим предложенную таблицу.

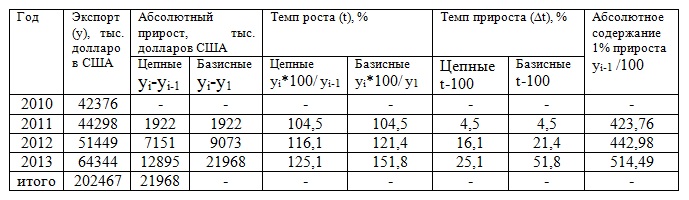Средний уровень ряда определим по средней арифметической простой: Уср=202467:4=50616,75 тыс. долларов США.

Среднегодовой абсолютный прирост определим по формуле:

= (64344-42376) / (4-1) = 7322,67 тыс. долларов США.

Среднегодовой темп роста определим по формуле:

= 3√(64344:42376) = 1,15=115%

Среднегодовой темп прироста определим по формуле:

=1,15-1=0,15=15%.

Задача 3. По следующей информации определить средний размер имущества
предприятия за квартал:

Решение

Средний размер имущества предприятия за квартал определим по формуле:

= (30/2 +40 +50 +30/2) / (4-1) = 40 млн. руб.

Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.
По форме представления — ряды абсолютных, относительных и средних величин.
По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.
По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).

Средние показатели ряда динамики

Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.

Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).

В случае интервального ряда его средний уровень определяется по формуле из уровней ряда, т.е.

=
Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода, т.е. как . Количество таких средних будет . Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать.
После преобразования числителя получаем,

Y1 Yn Yi

Эта средняя известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.

В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е..
В данном случае предполагается, что в промежутках между датами уровни принимали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода.
Если же предполагается, что каждое значение yi остается неизменным до следующего (i+1)-го момента, т.е. известна точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной:,

Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.

Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть

Б =

Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть

Ц =

По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.

Из следует, что базисное и цепное среднее изменение должны быть равными.

Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.

Базисное среднее относительное изменение определяется по формуле

Б==

Цепное среднее относительное изменение определяется по формуле

Ц=

Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.

Предыдущая лекция…

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде или , причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные и наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.