Сложение и вычитание дробей

Преобразование неправильной дроби в смешанное число

Любой неправильный дробь можно представить в виде натурального числа или суммы натурального числа и правильной дроби:

Для преобразования неправильной дроби в смешанное число необходимо:

1. поделить числитель дроби на его знаменатель;
2. остаток от деления записать в числитель, знаменатель оставить без изменений;
3. результат от деления записать целой частью.

Примеры преобразования неправильной дроби в смешанное число

Пример 1: Преобразовать неправильный дробь (выделить полную часть):

Целая часть равна 3, а остаток — 2

Ответ:

Пример 2: Преобразовать неправильный дробь (выделить полную часть):

Целая часть равна 67, а остаток — 1

Ответ:

Пример 3: Превратить неправильный дробь (выделить полную часть):

Целая часть равна 13, а остаток — 2

Ответ:

Преобразование обыкновенной дроби в десятичную

На практике чаще используют десятичные дроби, но, когда в задаче встречаются и обыкновенные, и десятичные дроби, то следует перейти к одному виду дробей (перевести десятичные дроби в обыкновенные или обыкновенные в десятичные). Не всегда обыкновенную дробь можно перевести в десятичную, поэтому десятичный переводят в обычный.

При переводе десятичной дроби в обычный в числителе дроби записывают число,что стоит после запятой, а разрядная единица в знаменателе ( и т.д.) содержит столько же нулей, сколько знаков после запятой в десятичной дроби.

Пример 4:Переведите обыкновенную дробь в десятичную

Если десятичная дробь содержит целую часть, то его переводят в смешанное число и целую часть записывают перед дробной:

Алгоритм решения задач с обыкновенной дробью общего вида

1. Когда необходимо произвести вычитание дробей с одинаковыми знаменателями, то в процессе решения суммируется только числитель дробей.\Где:\ и равные некоторым числовым значениям.
2. При выполнении сложения или вычитания дробей для  различных значений в  знаменателях, нужно выполнить приведение к общему знаменателю. Далее осуществить сложение или вычитание преобразованных дробей с одинаковыми числовыми значениями.
3. При перемножении дробных значений, выполняются следующие действия:
   • произведение числителей;
   • аналогичные действия , но только с знаменателями.
4. При выполнении деления, необходимо первую дробь перемножить на вторую, но в обратном значении. Иными словами произвести замену числителя на значение знаменателя.

Основные показатели и свойства дроби:

• черта в дроби обозначает признак деления;
• деление на числовое значение характеризуется как перемножение его   на обратное значение;
• возможность применения свойств, которые относятся для действительных чисел;
• свойства для дробей и различного рода числовых неравенств.

Применяя данные свойства можно произвести преобразование дробных чисел:

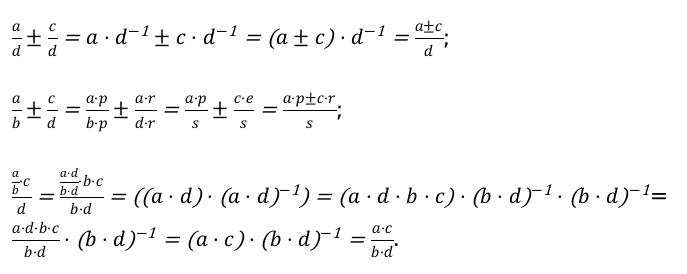
Пример №1:

Для заданных значений дроби: \ и \ необходимо выполнить сложение.

используя алгоритм решения, необходимо значения в числителе сложить, а в знаменателе оставить без изменений и переписать.

Выполнив все действия получим дробь: \.

Далее произведем сложение и получим дробное значение:

\

Следовательно: \

Ответ задачи: \.

Пример №2

Необходимо найти разность дробей:  

\

и

\{2}}{3 \cdot\left(\log_{2} 3 \cdot \log_{2} 5+1\right)}\]

Так как в знаменателе данные являются равными между собой. вычисление будет производиться по принципу равного знаменателя.

Из этого следует:

\{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}=\frac{1-\sqrt{2} \sqrt{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}\]

Для решения данного типа задач важно помнить правило приведения к общему знаменателю

Вычислительные действия с десятичными дробями

В свою очередь данный вид дробей подразделяется на следующие категории:

1. Конечные — если после запятой присутствует окончательное число.Например: \\
2. Бесконечные  — количество цифр после запятой, не имеют окончательного значения, то есть они бесконечны.Например: \\

Основные свойства дробей:

Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных для данного вида дробей.

Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.

 Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей

• 0,900 = 0,9;
• 22,10200000 = 22,102;
• 0,45000=0,45;
• 0,12569000=0,12569;
• 0,780=0,78.

Дроби — коротко о главном

Определения:

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Например: \(\displaystyle\frac{2}{5}\), \(\displaystyle\frac{1}{7}\) и так далее.

Например: \(\displaystyle\frac{9}{5}\), \(\displaystyle\frac{13}{2}\) и так далее.

Например: \(\displaystyle2\frac{2}{5}\)\( \displaystyle  \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}\).

Например: \(\displaystyle\frac{9}{100}\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac{225}{1000}\) записывается как \(\displaystyle0,225\).

Основное свойство дроби: 

Например: \(\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}\).

Действия с дробями:

Сложение/вычитание дробей

• две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: \(\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
• две обыкновенные дроби с разными знаменателями:
  • приводим дроби к наименьшему общему знаменателю;
  • складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
  • сокращаем полученную дробь
• две смешанные дроби с разными знаменателями: 
  • приводим дробные части этих чисел к наименьшему общему знаменателю;
  • по-отдельности складываем/вычитаем целые части и дробные части;
  • если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
  • сокращаем полученную дробь.

Умножение дробей

• умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
• умножение двух обыкновенных дробей: 
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь
• умножение двух смешанных чисел: 
  • преобразовываем смешанные дроби в неправильные;
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь;
  • если получилась неправильная дробь преобразовываем ее в смешанную.

Деление дробей

• деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
• деление натурального числа на дробь: число умножаем на дробь обратную данной
• деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
• деление двух смешанных чисел: 
  • преобразовываем смешанные дроби в неправильные;
  • умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.

Сокращение дроби

Например: \(\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}\).

Приведение дробей к наименьшему общему знаменателю

• найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
• разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
• умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.

Например: \(\displaystyle\frac{1}{3}\) и \(\displaystyle\frac{3}{4}\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}\), для второй дроби: \(\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}\).

Преобразования неправильной дроби в смешанную дробь

• поделите числитель дроби на ее знаменатель;
• остаток от деления запишите в числитель, знаменатель оставьте прежним;
• результат от деления запишите в качестве целой части.

Например: \(\displaystyle\frac{17}{4}\) = \(\displaystyle4\frac{1}{4}\).

Сравнение дробей:

• две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
• две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
• две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше

Сложение смешанного числа и обыкновенной дроби

Сложение смешанного числа и правильной дроби можно выполнить, прибавив к данной дроби дробную часть данного смешанного числа: .

Пример.

Выполните сложение обыкновенной дроби 5/12 и смешанного числа .

Решение.

.

Осталось выделить целую часть из неправильной дроби и завершить вычисления: .

Итак, сложение правильной дроби 5/12 и смешанного числа дает .

Ответ:

.

Сложение смешанного числа и неправильной обыкновенной дроби сводится к сложению двух смешанных чисел. Для этого достаточно выделить целую часть из неправильной дроби.

Пример.

Вычислите сумму .

Решение.

Для начала выделим целую часть из неправильной дроби 22/5, имеем . Теперь сложение смешанного числа и неправильной дроби приводится к сложению двух смешанных чисел: .

Ответ:

.

Список литературы.

• Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: учебник для 5 кл. общеобразовательных учреждений.
• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.

Сложение смешанных чисел

Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.

Сложение смешанного числа и натурального числа

Запоминаем
Чтобы сложить смешанное число и натуральное число, прибавьте натурально число к целой части смешанного числа, а дробную часть оставьте нетронутой.

Представим первое правило в виде буквенных выражений.

Выполним сложение смешанного числа и натурального числа d.

Известно, что любое смешанное число равное сумме целой и дробной частей.

Это значит, что .

Тогда .

Рассмотрим примеры сложения смешанных чисел с натуральными числами.

Пример 1. Выполните сложение смешанного числа и натурального числа 18.

Как решаем:

Записываем выражение

Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа и вычисляем: .

Ответ: .

Пример 2. Выполните сложение смешанного числа и натурального числа 10.

Как решаем:

Записываем выражение: .

.

Ответ: .

Пример 3. Выполните сложение смешанного числа и натурального числа 2.

Как решаем:

Записываем выражение:

.

Ответ: .

Сложение смешанного числа со смешанным числом

Запоминаем
Чтобы сложить смешанное число с другим смешанным числом, сложите сначала целые части этих чисел, а затем — дробные части.

Представим правило в виде буквенных выражений.

Выполним сложение смешанного числа и смешанного числа .

Следуя правилу, запишем выражение в виде: .

Рассмотрим примеры сложения смешанных чисел.

Пример 1. Сложите смешанное число и смешанное число .

Как решаем:

Записываем выражение: .

Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:

Решаем: складываем целые части 2 + 7 = 9.

Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.

.

Наименьшее общее кратное — 15.

.

Если в результате сложения получилась сократимая дробь, сокращайте, не задумываясь: сокращаем на .

.

Ответ: .

Пример 2. Сложите смешанное число и смешанное число .

Как решаем:

Записываем выражение: .

Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части: .

Решаем: складываем целые части 13 + 2 = 15.

Складываем дробные части

Наименьшее общее кратное 12 и 20 равно 60.

.

Сокращаем дробь на .

.

Ответ:

Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.

Сложение смешанного числа и правильной дроби

Запоминаем
Чтобы выполнить сложение смешанного числа и правильной дроби, прибавьте к дроби дробную часть смешанного числа, а целую часть оставьте без изменений.

Представим правило в виде буквенного выражения.

Если нам нужно сложить смешанное число и правильную дробь , то запишем следующее выражение: .

Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.

Пример 1. Выполните сложение обыкновенной дроби и смешанного числа

Как решаем:

Записываем выражение:

Согласно правилу, складываем дробь с дробной частью смешанного числа:

.

Складываем дроби .

Наименьшее общее кратное 5 и 20 равно 20.

, сокращаем на 5, получается .

.

Ответ: .

Пример 2. Выполните сложение правильной дроби и смешанного числа .

Как решаем:

Записываем выражение: .

Следуя правилу, складываем дробь с дробной частью смешанного числа:

.

Складываем дроби .

Наименьшее общее кратное 4 и 2 равно 4.

.

.

Ответ: .

Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.

Сложение многозначного числа с однозначным

Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.

Допустим, нам нужно найти сумму чисел 88 и 5.

Способ 1.

Представим число 88 в виде суммы 80+8 и прибавим к ней число 5. После этого, найдем сумму однозначных чисел 8 и 5, получится 13. Прибавим этот результат к числу 80. Число 13 – это 10+3, поэтому мы к 8 десяткам прибавляем 1 десяток, получаем 9 десятков, или число 90, а к нему прибавляем еще 3 (оставшиеся от числа 13), и получим 93.

То есть, мы проделываем такие действия:

88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.

Способ 2.

Замечаем, что если к 88 прибавить 2, то получим полный десяток, то есть, число 90. Тогда представляем число 5 в виде суммы 2+3; число 2 складываем с 88, получаем замеченное нами ранее число 90. Добавляем к нему оставшееся число 3, и получаем результат 93.

То есть, ход вычисления был такой:

88+5 = 88+2+3 = 90+3 = 93.

Интересные способы научить прибавлять и отнимать

Ребенок должен запомнить многие числовые комбинации. Чтобы помочь лучше понять этот материал, рекомендуется предложить ему следующие задачи:

• Рассортировать данное количество объектов в три тарелки, создав разные комбинации (варианты разные: повесить игрушки на две елки, расставить цветы в двух вазах, разместить гномов в двух домах);
• дополнить число до желаемого;
• заполнить ячейки, в которых записан состав с присвоенным номером;
• дорисовать домино.

Числовой ряд

Поможет усвоить устный счет игра в интервал между значениями. Мама говорит, что загадала определенное число в промежутке от 5 до 18. Ребенок должен угадать, если он ошибается, взрослый определяет место в ряду, регулируя поиски словами «больше», «меньше», «добавь один», «отними два».

Первые успехи

Ребенку будет сложно понять на уроках математику в первом классе, если он не усвоил технику счета. Терпение, игровые методы, непринужденность и регулярность упражнений это необходимые условия для успешного обучения. Даже одна десятая материала, усвоенного ребенком самостоятельно, поможет освоить школьную программу.

Простые дроби

В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.

Это простая дробь. 

Простые дроби принято записывать одним из следующих способов: \(\displaystyle \frac{1}{4}\), \(\displaystyle {1}/{4}\;.\)

Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту \(\displaystyle 1/4?\) Было \(\displaystyle 4\) из \(\displaystyle 4\), или \(\displaystyle 4/4\), забрали \(\displaystyle 1/4\).

Верно, останется \(\displaystyle 3\) дольки, \(\displaystyle 3\) из \(\displaystyle 4\). Запишем, как полагается, \(\displaystyle 3/4\).

Можно даже вот так: \(\displaystyle 4/4-1/4=3/4\)

То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.

Примеры простых дробей: \(\displaystyle 1/5,\text{ }2/4,\text{ }3/10,\text{ }17/3.\)

Правильные и неправильные простые дроби

В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например\(\displaystyle 17/3\).

Если числитель больше знаменателя, то дробь называется неправильной. 

Вне зависимости от того правильная дробь или неправильная, она будет простой.

Давай остановимся на неправильной дроби \(\displaystyle 17/3\). Что же это она неправильная?

Вспоминай пример с пирогом, там была \(\displaystyle 1/4\) – одна часть из четырех, а тут что получается? \(\displaystyle 17\) частей из \(\displaystyle 3\)?

Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем \(\displaystyle 4\) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.

А \(\displaystyle 17/3\)?

Что же, у нас есть \(\displaystyle 17\) частей, а для целого пирога в данном случае надо \(\displaystyle 3\) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.

Как узнать сколько пирогов мы можем получить из \(\displaystyle 17\) частей? Верно, надо на \(\displaystyle 3\) как раз и поделить.

Если попробовать составить \(\displaystyle 6\) пирогов, т.е. \(\displaystyle 3\cdot 6=18\), надо \(\displaystyle 18\) частей. Не хватает. А \(\displaystyle 3\cdot 5=15\), о, хватило! Получается \(\displaystyle 5\) целых пирогов собрали, положили в сторону. Осталось \(\displaystyle 17-3\cdot 5=2,2\), \( \displaystyle  2\) куска.

А для целого пирога надо \( \displaystyle  3\) части. В итоге у нас \( \displaystyle  5\) целых и \( \displaystyle  2/3\) (две третьих) пирога.

Много места занимает такое обозначение. А что если убрать лишние слова и оставить только \( \displaystyle  5\frac{2}{3}\) (пять целых и две третьих).

Как объяснить связь сложения и вычитания

Для лучшего восприятия следует научить малыша составу. Методика заключается в трех шагах:

1. На привычных предметах усвоить, что одно из слагаемых может меняться в сторону уменьшения, другое возрасти при одинаковой сумме. Удачным пособием станут упаковки для яиц (по 10); боксы для печенья (по 6,8 или 12), календарные дни (по 7).
2. Следует проследить, чтобы ребенок сделал записи в тетради по возможным комбинациям числительных.
3. Вместе с учеником подготовить карточки с надписями: 6 + 3 = 9; 4 + 5 = 9; 2 + 7 = 9; 1 + 8 = 9. Лучше распределить каждый пример на отдельную карточку.

Теперь нужно приложить усилия к запоминанию. Ребенок должен наизусть, не считая, запомнить все возможные комбинации слагаемых, дающих одну сумму. Не нужны длинные занятия. Успех придет быстрее, когда урок на запоминание будет быстрым, как перерыв между лепкой или рисованием.

Связь между сложением и вычитанием

Если ребенок все запомнил и не пытается «посчитать», можно приступать к следующему шагу. При замене знакомых карточек новыми, малыш должен писать сразу ответы. Приступаем к самому сложному – вычитать, используя знание составляющих. Вначале необходимо повторить карточки с действиями. Потом нужно спросить у ребенка, что будет с результатом, если убрать одно из слагаемых.

Данная цепочка поможет оценить связь сложения с вычитанием методом запоминания. Ученик должен понять, что вспомнить знакомое сочетание легче, чем считать в уме. В дальнейшем принцип поможет легче освоить решение линейных уравнений.

Сложение чисел с разными знаками

Рассмотрим ситуацию.

Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?

Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.

Суммируем-3 и 10. Для этого:

• определяем модули: -3=|3|, 10=|10|;
• сравниваем модули, определяя больший: |3|<|10|;
• от большего отнимаем меньший: 10 – 3=7;
• так как по условию 10 – число положительное, то и результат будет числом положительным.

Записывается в таком виде:

-3+10=10 – 3=7.

Выходит, у мальчика стало 7 яблок.

Рассмотрим еще один пример сложения чисел с разными знаками.

Вычислите сумму -28 и 11.

Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.

-28=|28|;

11=|11|;

28>11.

Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:

-28+11=-(28-11)=-17.

Учитывая рассмотренные примеры, можно сказать, что:

любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.

Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.

Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:

-150+50=-(150-50)=-100.

Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:

При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.

-150=|150|;

-100=|100|.

150>100;

-150<-100.

Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.

Вычитание алгебраических дробей

Запомните!

Вычитать можно только дроби с одинаковыми знаменателями!

При вычитании алгебраических дробей с одинаковыми знаменателями:

1. из числителя первой дроби вычитается числитель второй дроби.
2. знаменатель остаётся прежним.

Важно!

Обязательно заключите в скобки весь числитель вычитаемой дроби.

Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.

Рассмотрим пример вычитания алгебраических дробей.

Так как у обеих алгебраических дробей знаменатель «», значит, эти дроби можно вычитать.

Вычтем из числителя первой дроби «» числитель второй дроби
«».
Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем
.

Решение легких задач с применением метода вычитания

Задача № 1

\

Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:

\

\

\

\

Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:

\

\

\

\

Ответ: $\left( 2;5 \right)$.

Задача № 2

\

Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:

\

\

\

Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:

\

\

\

\

\

Ответ: $\left( -3;-2 \right)$.

Нюансы решения

Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.

Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.

Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.

Зачем решать типовые задачи?

Знакомясь с типовыми задачами, отрабатывая единый алгоритм их решения, ребенок учится совершать шаги, которые называют универсальными учебными действиями (УУД): умение поставить задачу, выбрать способы решения, проанализировать полученные результаты и т. д

Эти действия впоследствии ребенок будет совершать не только на уроках математики, поэтому овладение ими чрезвычайно важно. Это и есть цель решения типовых задач

Процесс овладения УУД делится на 2 этапа: 1) формирование УУД; 2) применение УУД.

Первый этап обучающиеся проходят еще в начальной школе. Именно в это время в память закладываются базовые навыки решения задач. Начиная с 5 класса ребенок учится применять эти навыки для решения конкретной задачи.