Интересные факты о жизни евклида, биография, наследие

Достижения Евклида

Достижения Евклида имели огромное значение для мировой истории, математики и других наук.

Он был первым, кто:

систематизировал известные труды предшественников в единый сборник из 13 книг,
создал 5 постулатов НОД и 5 аксиом в области геометрии,
охарактеризовал все известные геометрические фигуры, дал понятие кривым линиям, коническим сечениям и другим явлениям,
создал трактат по ошибкам при изучении и создании геометрических доказательств,
доказал практическое использовании математики при изучении звезд, небесных тел, космоса и других наук,
изучил свет с законами его распространения,
изучил зеркала и способности преломления в них световых лучей,
создал простейшую теорию в области музыки,
создал постулаты и формулы по механики и определил удельный вес тел.

Математика

Евклид отец математики. Он сформулировал теоремы по планиметрии, упростил понимание теоремы Пифагора и теоремы о сумме углов треугольника, прописал свойства правильных многоугольников и законы построения правильных пятнадцатиугольников, указал, как применима алгебры в жизни и каковы ее основные теории, вписал теорию о целом и рациональном числе, рассмотрел квадратичную иррациональность, заложил основы стереометрической науки, доказал теоремы, касающиеся площади круга с объемом шара, вывел отношение объема пирамид с конусами, призмами и цилиндрами.

Другие науки

Помимо математики, ученый работал с оптикой, астрономией, логикой и музыкой. Так, в оптике он дал сведения об оптической перспективе, зеркальных искажениях и отражениях световых лучей в зеркале.

Другие работы

Построение Евклидом регулярного додекаэдр.

Построение додекаэдра путем размещения граней на ребрах куба.

В добавок к Элементы, до наших дней сохранилось как минимум пять произведений Евклида. Они следуют той же логической структуре, что и Элементы, с определениями и доказанными предложениями.

Данные рассматривает природу и значение «данной» информации в геометрических задачах; тема тесно связана с первыми четырьмя книгами Элементы.
О делениях фигур, который выживает лишь частично в арабский перевод, касается разделения геометрических фигур на две или более равные части или на части в данном соотношения. Это похоже на работу первого века нашей эры. Цапля Александрийская.
Катоптрики, которая касается математической теории зеркал, в частности изображений, формируемых в плоских и сферических вогнутых зеркалах. Приписывание авторства считается анахронизмом, однако Дж. Дж. О’Коннор и Э. Ф. Робертсон, которые называют Теон Александрийский как более вероятный автор.
Феномены, трактат о сферическая астрономия, выживает на греческом языке; это очень похоже на В движущейся сфере к Автолик Питанский, который процветал около 310 г. до н. э.

Статуя Евклида XIX века. Автор Джозеф Дарем в Музей естественной истории Оксфордского университета

Оптика это самый ранний из сохранившихся греческих трактатов о перспективе. В своих определениях Евклид следует платонической традиции, согласно которой видение вызвано дискретные лучи, исходящие из глаза. Одним из важных определений является четвертое: «То, что видно под большим углом, кажется больше, а под меньшим углом — меньше, в то время как предметы под равным углом кажутся равными». В следующих 36 предложениях Евклид связывает видимый размер объекта с его расстоянием от глаза и исследует видимые формы цилиндров и колбочек, если смотреть под разными углами. Предложение 45 интересно тем, что доказывает, что для любых двух неравных величин существует точка, в которой они кажутся равными. Паппус считал эти результаты важными в астрономии и включал в себя Евклидов Оптикавместе с его Феномены, в Маленькая астрономия, сборник небольших работ, которые нужно изучить перед Синтаксис (Альмагест) из Клавдий Птолемей.

Утраченные работы

Другие работы достоверно приписываются Евклиду, но были утеряны.

Коники была работа над конические секции который позже был расширен Аполлоний Пергский в его знаменитую работу по этому вопросу. Вполне вероятно, что первые четыре книги творчества Аполлония исходят непосредственно от Евклида. По словам Паппа, «Аполлоний, завершив четыре книги коников Евклида и добавив четыре других, передал восемь томов коников». Коники Аполлония быстро вытеснили прежнюю работу, и ко времени Паппа работа Евклида была уже потеряна.
Поризмы возможно, было следствием работы Евклида с коническими сечениями, но точный смысл названия является спорным.
Псевдария, или же Книга заблуждений, был элементарный текст об ошибках в рассуждение.
Поверхностные локусы обеспокоен либо места (наборы точек) на поверхностях или локусах, которые сами были поверхностями; при последней интерпретации была выдвинута гипотеза, что работа могла иметь дело с квадратичные поверхности.
Несколько работ по механика приписываются Евклиду арабскими источниками. О тяжелом и легком содержит в девяти определениях и пяти предложениях аристотелевские понятия движущихся тел и понятие удельного веса. На весах трактует теорию рычага аналогично евклидовой манере, содержащей одно определение, две аксиомы и четыре предложения. Третий фрагмент на кругах, описываемых концами подвижного рычага, содержит четыре предложения. Эти три работы дополняют друг друга таким образом, что было высказано предположение, что они являются остатками единого трактата по механике, написанного Евклидом.

Постулаты Евклида

Его главная книга «Элементы» (первоначально написанная на древнегреческом языке) стала базовой работой важных математических учений. Она разделена на 13 отдельных книг.

Книги от первой до шестой посвящены геометрии плоскости.
Книги семь-девять имеют дело с теорией чисел
Книга восьмая о геометрической прогрессии
Книга десятая посвящена иррациональным числам
Книги одиннадцать-тринадцать представляют собой трехмерную геометрию (стереометрию).

Гений Евклида состоял в том, чтобы взять в оборот множество разнообразных элементов математических идей и объединить их в один логический, последовательный формат.

Лемма Евклида, которая утверждает, что фундаментальное свойство простых чисел состоит в том, что если простое число делит произведение двух чисел, оно должно делить по крайней мере одно из этих чисел.

Научные достижения

Первое научное сочинение.

Самое первое собрание научных сочинений, посвященное теме математики, было создано именно Эвклидом более чем 2 тысячи лет назад.

Развитие геометрии.

Эвклид поспособствовал развитию современной геометрии. Он посвятил 4 книги коническим сечениям.

«Начала».

Один из самых важных научных трудов великого математика — «Начала», содержавшая в себе все знания о планиметрии, стереометрии и теории чисел. Сборник книг не утратил свою популярность и в наше время. Интересно, что существуют и другие труды с таким же названием, но евклидовые «Начала» являются самыми известными и популярными. «Начала» включат в себя 13 отдельных книг, написанных самим Эвклидом, а также еще 2 книги, авторами которых являются Исидор и Гипсикл.

В России «Начала» были переведены лишь в 18 веке, а в Армении — уже в 11.

Эвклидова геометрия.

Геометрия, изучаемая в рамках школьной программы, и в наше время носит имя Эвклида.

Древние труды.

Эвклиду приписано очень много трудов, авторство которых не установлено. Эти труды относятся к самым разным областям, например, к музыке и медицине. Доказательств того, что эти работы принадлежат древнегреческому ученому нет, но многие историки, что автором является именно он.

Три геометрии.

В мире есть 3 геометрии: Эвклида, Лобачевского и Ремана. Самой популярной и распространенной является первая

Оптика и астрономия.

Научно доказано, что ученый прекрасно разбирался не только в математике, но и в оптике и астрономии. Об этом утверждают его научные труды, связанные с этими областями.

Теории и аксиомы.

Все теории и аксиомы сохранились в первоначальном виде. Аксиомы древнегреческого математика активно используются и изучаются и в наше время. Например, аксиома о параллельности прямых принадлежит именно ему.

Образец научного труда.

Труды Эвклида считаются образцом и по сей день. Связано это с тем, что в его собраниях научных сочинений все систематизировано и логически связано друг с другом.

Другие работы математика.

Кроме знаменитых «Начал» древнегреческому ученому принадлежат такие научные труды, как «Данные», «Явления», «О делении фигур».

Отец геометрии.

Эвклид по праву считается отцом геометрии, ведь именно он сумел систематизировать все полученные на тот момент математические знания. Он упорядочил все законы, принципы, теории и аксиомы, тем самым упростил изучение науки.

Научная деятельность

Евклида обоснованно считают «отцом геометрии». Именно он заложил основы этой области знаний и возвёл её на должный уровень, открыв обществу законы одного самых сложных разделов математики в то время. После переезда в Александрию, Евклид, как и многие учёные того времени, благоразумно проводит большую часть времени в Александрийской библиотеке. Этот музей, посвящённый литературе, искусству и наукам, был основан ещё Птолемеем. Здесь Евклид начинает объединять геометрические принципы, арифметические теории и иррациональные числа в единую науку геометрию. Он продолжает доказывать свои теоремы и сводит их в колоссальный труд «Начала». За всё время своей малоисследованной научной деятельности, учёный закончил 13 изданий «Начал», охватывающих широкий спектр вопросов, начиная с аксиом и утверждений и заканчивая стереометрией и теорией алгоритмов. Наряду с выдвижением различных теорий, он начинает разрабатывать методику доказательства и логическое обоснование этих идей, которые докажут предложенные Евклидом утверждения.

Его труд содержит более 467 утверждений касательно планиметрии и стереометрии, а также гипотез и тезисов, выдвигающих и доказывающих его теории относительно геометрических представлений. Доподлинно известно, что в качестве одного из примеров в своих «Началах» Евклид использовал теорему Пифагора, устанавливающую соотношение между сторонами прямоугольного треугольника. Евклид утверждал, что «теорема верна для всех случаев прямоугольных треугольников». Известно, что за время существования «Начал», вплоть до XX века, было продано больше экземпляров этой книги, чем Библии. «Начала», изданные и переизданные бесчисленное количество раз, в своей работе использовали разные математики и авторы научных трудов. Евклидова геометрия не знала границ, и учёный продолжал доказывать всё новые теоремы в совершенно разных областях, как, например, в области «простых чисел», а также в области основ арифметических знаний. Цепочкой логических рассуждений Евклид стремился открыть тайные знания человечеству. Система, которую учёный продолжал разрабатывать в своих «Началах», станет единственной геометрией, которую будет знать мир вплоть до XIX века. Однако современные математики открыли новые теоремы и гипотезы геометрии, и разделили предмет на «евклидову геометрию» и «неевклидову геометрию».

Сам учёный называл это «обобщённым подходом», основанным не на методе проб и ошибок, а на представлении неоспоримых фактов теорий. Во времена, когда доступ к знаниям был ограничен, Евклид принимался за изучение вопросов совершенно разных областей, в том числе и «арифметики и чисел». Он заключил, что обнаружение «самого большого простого числа» физически невозможно. Это утверждение он обосновал тем, что, если к самому большому известному простому числу добавить единицу, это неизбежно приведёт к образованию нового простого числа. Этот классический пример является доказательством ясности и точности мысли учёного, несмотря на его почтенный возраст и времена, в которые он жил.

ссылки

Бисон М. Брауэр и Евклид. Indagationes Mathematicae. 2017; 51: 1-51.
Корнелиус М. Евклид должен идти ? Математика в школе. 1973; 2(2): 16-17.
Флетчер В. К. Евклид. Математическая газета 1938: 22(248): 58-65.
Флориан С. Евклид Александрийский и бюст Евклида Мегарского. Наука, Новая серия. 1921; 53(1374): 414-415.
Эрнандес Й. Более двадцати веков геометрии. Журнал Книги. 1997; 10(10): 28-29.
Медер А. Е. Что не так с Евклидом?? Учитель математики. 1958; 24(1): 77-83.
Тейсен Б. Ю. Евклид, Относительность и парусный спорт. История Mathematica. 1984; 11: 81-85.
Валле Б. Полный анализ бинарного евклидова алгоритма. Международный симпозиум по алгоритмической теории чисел. 1998; 77-99.

биография

Точная дата рождения Евклида неизвестна. Исторические записи позволили определить его местонахождение где-то в 325 году до нашей эры..

По его образованию, по оценкам, имело место в Афинах, потому что работа Евклида показала, что он глубоко знал геометрию, которая была создана из школы Платона, разработанной в этом греческом городе.

Этот аргумент поддерживается до тех пор, пока не будет выведено, что Евклид, казалось, не знал работы афинского философа Аристотеля; по этой причине нельзя утверждать окончательно, что образование Евклида было в Афинах.

Преподавательская работа

В любом случае известно, что Евклид учил в Александрии, когда командовал королем Птолемеем I Сотером, который основал династию Птолемеев. Считается, что Евклид проживал в Александрии около 300 г. до н.э., и там он создал школу, посвященную преподаванию математики..

В этот период Евклид приобрел большую известность и признание благодаря своим способностям и навыкам учителя..

Анекдот, связанный с королем Птолемеем I, выглядит следующим образом: некоторые записи указывают, что этот король попросил Евклида научить его быстрому и краткому способу понимания математики, чтобы понимать и применять их.

Учитывая это, Евклид указал, что нет никаких реальных способов получить это знание. Намерение Евклида с этим двойным смыслом состояло также в том, чтобы показать царю, что, будучи не могущественным и привилегированным, может понимать математику и геометрию.

Личные характеристики

Вообще, Евклид изображался в истории как спокойный, очень добрый и скромный человек. Также сказано, что Евклид полностью понимал огромную ценность математики, и что он был убежден, что знание само по себе бесценно.

На самом деле, есть еще один анекдот об этом, который превзошел наше время благодаря доктору Хуану де Эстобео.

По-видимому, на уроке Евклида, в котором рассматривался предмет геометрии, студент спросил его, какую пользу он получит, получив эти знания. Евклид твердо ответил ему, объяснив, что знание само по себе является самым бесценным элементом, который существует.

Поскольку ученик, очевидно, не понимал и не подписывался на слова своего учителя, Евклид дал указание своему рабу дать ему несколько золотых монет, подчеркнув, что выгода от геометрии была гораздо более превосходной и глубокой, чем денежное вознаграждение..

Кроме того, математик указал, что нет необходимости получать прибыль от каждого знания, приобретенного в жизни; Сам факт получения знаний сам по себе является величайшим достижением. Это было видение Евклида в отношении математики и, в частности, геометрии.

смерть

Согласно записям в истории, Евклид умер в 265 году до нашей эры в Александрии, городе, в котором он прожил большую часть своей жизни..

Вклад в науку

Почти со времени написания его основной труд оказывал постоянное и значительное влияние. Это был основной источник геометрических рассуждений, теорем и методов, по крайней мере, до появления неевклидовой геометрии в 19-м веке. Иногда говорят, что, помимо Библии, «Начала» являются самыми часто переводимыми, публикуемыми и изучаемыми из всех книг, выпущенных в западном мире. Если исходить из его биографии, Евклид, возможно, не был первоклассным математиком, но он установил стандарт для дедуктивного мышления и геометрического обучения, который сохранялся практически без изменений в течение более 2000 лет.

Истории из жизни

«Зачем вообще нужна геометрия?»

Эвклид занимался обучением детей, у него была математическая школа. Однажды его ученик поинтересовался, кому и зачем вообще нужна геометрия, что она может дать в дальнейшем. Выслушав вопрос, Эвклид дал мальчишке 3 золотых монеты и прогнал с урока (вероятно, такую сумму заплатили родители ученика за обучение). Он решил сразу дать прибыль ученику, если от геометрии ему нужна была лишь личная выгода.

«В геометрии нет царских путей».

Данная фраза относится к одной интересной легенде из жизни математика. Однажды царь захотел освоить начала геометрии и за основу взял труды Эвклида. Освоить науку царю не удавалось, а на свой вопрос о том, есть ли более простые пути изучения геометрии, получил такой ответ: «В геометрии нет царских путей».

Смерть и наследие

Год и причины смерти Евклида остаются для человечества тайной. В литературе встречаются туманные намёки на то, что он мог умереть около 260 г. до н.э. Наследие, оставленное учёным после себя, куда более значимо, чем впечатление, которое он производил при жизни. Его книги и труды продавались по всему миру до самого XIX века. Наследие Евклида пережило учёного на целых 200 веков, и служило источником вдохновения для таких личностей, как, например, Авраам Линкольн. По слухам, Линкольн всегда суеверно носил при себе «Начала», и во всех своих речах цитировал работы Евклида. Даже после смерти учёного, математики разных стран продолжали доказывать теоремы и издавать труды под его именем. В общем и целом, в те времена, когда знания были закрыты для широких масс, Евклид логическим и научным путём создал формат математики древности, который в наши дни известен миру под названием «евклидовой геометрии».

Личная жизнь

До нас дошла лишь некоторая информация о работе Евклида в науке, о его личной жизни же неизвестно практически ничего. Существует легенда, что царь Птолемей, решивший изучить геометрию, был раздосадован ее сложностью. Тогда он обратился к Евклиду и попросил его указать на более легкий путь к знаниям, на что мыслитель ответил: «К геометрии нет царской дороги». Выражение впоследствии стало крылатым.

Евклид основал математическую школу при Александрийской библиотеке

Есть доказательства того, что при Александрийской библиотеке этот древнегреческий ученый основал частную математическую школу. В ней учились такие же энтузиасты науки, как и сам Евклид. Даже на закате своей жизни Евклид помогал ученикам в написании работ, создании собственных теорий и разработке соответствующих доказательств.

Точных данных о внешности ученого нет. Его портреты и скульптуры – это плод воображения их создателей, придуманный образ, передававшийся из поколения в поколение.

Вычислительный Евклид

Элементы Евклида разделены на 13 «книг», содержащих в общей сложности 465 теорем и 131 определение.

Как известно, элементы математика Евклида представляли на протяжении веков саму модель научного и дедуктивного рассуждения, а их распространение и влияние в Европе были только в соответствии с Библией и несколькими другими писаниями церкви. Они переводились, редактировались и комментировались сотни раз, и эти издания и комментарии формировали научный инструментарий, методологические стандарты и математический язык многих веков.

Теоремы Евклида использовались для построения дальнейших и более смелых математических теорий или применялись в физических науках, в то время как структура доказательств изучалась математиками, логиками и эпистемологи как идеал самого разума. В этой связи особую историческую роль сыграли принципы, служившие основанием и фундаментом всего строительства.

Математик Евклид начал формулировать свои элементы с нескольких недоказанных предположений для того, чтобы установить великую математическую систему. Однако в античности система принципов Евклида неоднократно обсуждалась и оспаривалась: были найдены некоторые пробелы в доказательствах и недостающие аргументы, снабженные дополнительными аксиомами. Некоторые принципы были доказаны с помощью более простых способов или изменены, чтобы удовлетворить философские сомнения или удовлетворить архитектурные соображения. Еще несколько были добавлены, чтобы расширить геометрические результаты за пределы границ, установленных Евклидом. Эти изменения в системе принципов, лежащих в основе элементарной математики, были одними из наиболее важных результатов фундаментальных исследований, проведенных в позднем Средневековье XIV—XV вв.

Книги II—XIII

II книга — теоремы так называемой «геометрической алгебры».

III книга — предложения об окружностях, их касательных и хордах, центральных и вписанных углах.

IV книга — предложения о вписанных и описанных многоугольниках, о построении правильных многоугольников.

V книга — общая теория отношений, разработанная Евдоксом Книдским.

VI книга — учение о подобии геометрических фигур. Эта книга завершает евклидову планиметрию.

VII, VIII и IX книги посвящены теоретической арифметике. Евклид в качестве чисел рассматривает исключительно натуральные числа; для него «Число есть совокупность единиц». Здесь излагаются теория делимости и пропорций, доказывается бесконечность множества простых чисел, приводится алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, строятся чётные совершенные числа. Евклид доказывает также формулу для суммы геометрической прогрессии.

X книга — классификация несоизмеримых величин. Это самая объёмная из книг «Начал».

XI книга — начала стереометрии: теоремы о взаимном расположении прямых и плоскостей; теоремы о телесных углах, объём параллелепипеда и призмы, теоремы о равенстве и подобии параллелепипедов.

XII книга — теоремы о пирамидах и конусах, доказываемые с помощью метода исчерпывания. Здесь доказывается, например, теорема о том, что объём конуса составляет одну треть от объёма цилиндра с теми же основанием и высотой.

XIII книга — построение правильных многогранников; доказательство того, что существует ровно пять правильных многогранников.

Евклид нигде в книге не ссылается на других греческих математиков, хотя несомненно опирается на их результаты. Историки науки показали, что прототипом для труда Евклида послужили более ранние сочинения античных математиков:

Книги I—IV и XI — «Начала» Гиппократа Хиосского.
Книги V—VI и XII — труды Евдокса Книдского.
Книги VII—IX — сочинения Архита Тарентского и других пифагорейцев. По мнению Ван дер Вардена, это самая древняя по содержанию часть «Начал», восходящая к V веку до н. э.
Книги X и XIII — труды Теэтета Афинского.

Вопрос о том, содержат ли «Начала» какие-либо результаты самого Евклида или автор занимался только систематизацией и унификацией накопленных знаний, является предметом дискуссий. Есть предположение, что алгоритм построения правильного 15-угольника разработан Евклидом; вероятно, он же произвёл отбор и окончательную формулировку аксиом и постулатов.

В целом содержание «Начал» покрывает значительную часть античной теоретической математики. Однако некоторая часть известного древнегреческим математикам материала осталась вне этого труда — например, конические сечения (Евклид посвятил им отдельный труд, который не сохранился), длина окружности, теория приближённых вычислений.

Евклид

Евклид Родился: около 325 года до н. э.
Умер: до 265 года до н. э.

Биография

Евклид или Эвклид (др.-греч. Εὐκλείδης, от «добрая слава», время расцвета — около 300 года до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения о Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в 3 в. до н. э.

Евклид — первый математик Александрийской школы. Его главная работа «Начала» (Στοιχεῖα, в латинизированной форме — «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию Древнегреческой математики и создал фундамент дальнейшего развития математики. Из других сочинений по математике надо отметить «О делении фигур», сохранившееся в арабском переводе, 4 книги «Конические сечения», материал которых вошёл в произведение того же названия Аполлония Пергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Паппа Александрийского. Евклид — автор работ по астрономии, оптике, музыке и др.

Дополнительные штрихи к портрету Евклида можно почерпнуть у Паппа и Стобея. Папп сообщает, что Евклид был мягок и любезен со всеми, кто мог хотя бы в малейшей степени способствовать развитию математических наук, а Стобей передаёт ещё один анекдот о Евклиде. Приступив к изучению геометрии и разобрав первую теорему, один юноша спросил у Евклида: «А какая мне будет выгода от этой науки?» Евклид подозвал раба и сказал: «Дай ему три обола, раз он хочет извлекать прибыль из учёбы». Историчность рассказа сомнительна, поскольку аналогичный рассказывают о Платоне.

Некоторые современные авторы трактуют утверждение Прокла — Евклид жил во времена Птолемея I Сотера — в том смысле, что Евклид жил при дворе Птолемея и был основателем Александрийского Мусейона. Следует, однако, отметить, что это представление утвердилось в Европе в XVII веке, средневековые же авторы отождествляли Евклида с учеником Сократа философом Евклидом из Мегар.

Арабские авторы считали, что Евклид жил в Дамаске и издал там «Начала» Аполлония. Анонимная арабская рукопись XII века сообщает:

Евклид, сын Наукрата, известный под именем «Геометра», учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира…

В целом количество данных о Евклиде настолько скудно, что существует версия (правда, малораспространенная) что речь идет о коллективном псевдониме группы александрийских ученых.

Евклид и античная философия

Уже со времён пифагорейцев и Платона арифметика, музыка, геометрия и астрономия (так называемые «математические» науки; позже Боэцием названные квадривием) рассматривались в качестве образца систематического мышления и предварительной ступени для изучения философии. Не случайно возникло предание, согласно которому над входом в платоновскую Академию была помещена надпись «Да не войдёт сюда не знающий геометрии».

Геометрические чертежи, на которых при проведении вспомогательных линий неявная истина становится очевидной, служат иллюстрацией для учения о припоминании, развитого Платоном в Меноне и других диалогах. Предложения геометрии потому и называются теоремами, что для постижения их истины требуется воспринимать чертёж не простым чувственным зрением, но «очами разума». Всякий же чертёж к теореме представляет собой идею: мы видим перед собой эту фигуру, а ведём рассуждения и делаем заключения сразу для всех фигур одного с ней вида.

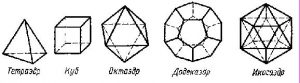
Некоторый «платонизм» Евклида связан также с тем, что в Тимее Платона рассматривается учение о четырёх элементах, которым соответствуют четыре правильных многогранника (тетраэдр — огонь, октаэдр — воздух, икосаэдр — вода, куб — земля), пятый же многогранник, додекаэдр, «достался в удел фигуре вселенной». В связи с этим Начала могут рассматриваться как развёрнутое со всеми необходимыми посылками и связками учение о построении пяти правильных многогранников — так называемых «платоновых тел», завершающееся доказательством того факта, что других правильных тел, кроме этих пяти, не существует.

Для аристотелевского учения о доказательстве, развитого во Второй аналитике, Начала также предоставляют богатый материал. Геометрия в Началах строится как выводная система знаний, в которой все предложения последовательно выводятся одно за другим по цепочке, опирающейся на небольшой набор начальных утверждений, принятых без доказательства. Согласно Аристотелю, такие начальные утверждения должны иметься, так как цепочка вывода должна где-то начинаться, чтобы не быть бесконечной. Далее, Евклид старается доказывать утверждения общего характера, что тоже соответствует любимому примеру Аристотеля: «если всякому равнобедренному треугольнику присуще иметь углы, в сумме равные двум прямым, то это присуще ему не потому что он равнобедренный, а потому что он треугольник» (An. Post. 85b12).