Методики деления
Деление чисел бывает с остатком и без него. Следовательно, для каждого направления существует собственный алгоритм. Необходимо разобрать основные отличия методик. Если операция выполняется нацело, то обязательно нужно проверить условие, воспользовавшись признаками деления двух величин.
При делении с остатком проверка по правилам делимости не требуется. Следует отметить, что данный тип операции применяется во многих дисциплинах. Примером одной из них является информатика. В ней используется перевод числа одной системы счисления (десятичной) в другую (двоичную, восьмеричную или шестнадцатеричную). Поэтому необходимо знать основной принцип и порядок применения алгоритма.
Перед применением одной из методик рекомендуется ознакомиться с разрядной сеткой. Она представляется собой набор цифр, расположенных на определенных позициях. Например, величина 1473 состоит из следующих компонентов:
- Тысячи: 1.
- Сотни: 4.
- Десятки: 7.
- Единицы: 3.
Следует отметить, что разложение на элементы начинается со старших разрядов, а затем заканчивается младшими. Это рекомендуется делать для того, что не допускать ошибок во время выполнения арифметических операций, таких как: сложение, произведение и вычитание. Кроме того, правильная запись пригодится при изучении более сложных дисциплин (информатики и программировании).
Алгоритм целого частного
Для выполнения операции деления в столбик нацело необходимо разбить число на разряды (по одному при однозначном делителе). Алгоритм рекомендуется рассматривать сразу на примере с величинами 1326 и 6. Он имеет такую реализацию:
- Записать число: 1326.
- Проверить его делимость на 6: 1+3+2+6=12 (+) и на 2 тоже.
- Взять разряд тысяч: 1<6 — необходима еще цифра, поскольку делимое должно быть больше делителя.
- Комбинация разрядов тысяч и сотен: 13.
- Разделить величину в четвертом пункте на 6: 13/6=2 (+1 остаток).
- Единица на 6 не делится. Нужно взять еще разряд: 12.
- Поделить значение, полученное на шестом шаге на 6: 12/6=2.
- Перенести разряд единиц и поделить его на шесть: 6/6=1.
- Записать искомое частное: 221.
- Проверка: 221*6=1326.
Операция с остатком
Операция получения частного двух чисел с остатком похожа на деление нацело, но есть некоторые особенности. Для этого необходимо рассмотреть ее алгоритм, который имеет такой вид:
- Взять I старший разряд и сопоставить его с делителем. Если он больше, то подобрать соответствующий множитель. В противном случае — перенести следующий элемент разрядной сетки, а затем осуществить подбор сомножителя.
- Записать первый разряд частного в графе результата.
- Перенести вниз следующий разряд. При необходимости его можно дополнить еще одним элементом.
- Подобрать следующий множитель, а затем умножить его на делитель.
- Осуществить операцию разности между элементами на третьем шаге и четвертом.
- При необходимости повторить операции, начиная с первого пункта методики и заканчивая пятым.
- Выполнить проверку посредством произведения делителя на частное.
Однако алгоритм необходимо реализовать на примере. Это выглядит следующим образом:
- Необходимо разделить 1341 на 2.
- Запись I неполного делимого: 1. Величина не подходит, поскольку 1<2.
- Перенос следующего разряда: 13.
- Деление: 13/2=6 (+1). Записать в графу результата величину 6.
- Остаток 1 не делится на 2. Необходимо добавить еще один элемент: 14.
- Перенести последний элемент: 1<2. Следовательно, 1 — остаток. В графу ставится нуль.
- Частное: 670 (+1).
- Проверка: 670*2+1=1341.
https://youtube.com/watch?v=yYBnWjRjPqg
Таким образом, деление многозначного числа на однозначное выполняется по определенной методике, результатом которой может быть частное с остатком или без него.
Представление делимого в виде произведения
При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель.
Рассмотрим типичные случаи.
Пример 2. Представление делимого в виде произведения
Разделим 30 на 3.
Делимое 30 можно представить в виде произведения30=3·10.
Имеем: 30÷3=3·10÷3
Воспользовавшись свойством деления произведения двух чисел, получаем:
3·10÷3=3÷3·10=1·10=10
30÷3=10
Приведем еще несколько аналогичных примеров.
Пример 3. Представление делимого в виде произведения
Вычислим частное 7200÷72.
Представляем делимое в виде 7200=72·100. При этом, результат деления будет следующим:
7200÷72=72·100÷72=72÷72÷100=100
Пример 4. Представление делимого в виде произведения
Вычислим частное: 1600000÷160.
1600000=160·10000
1600000÷160=160·10000÷160=160÷160·10000=10000
В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.
Пример 5. Представление делимого в виде произведения
Разделим 5400 на 9.
Таблица умножения подсказывает нам, что 54 делится на 9, поэтому делимое целесообразно представить в виде произведения:
5400=54·100.
Теперь закончим деление:
5400÷9=54·100÷9=54÷9·100=6·100=600
Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.
Пример 6. Представление делимого в виде произведения
Посчитаем, сколько будет 120 разделить на 4.
120=12·10
120÷4=12·10÷4=12÷4·10=3·10=30
Общие принципы построения
на другое натуральное число Для этого будем строить последовательность натуральных чисел:
такую, что:
- каждый член последовательности вполне определяется предыдущим;
- последний член последовательности меньше то есть
- все члены последовательности являются равноделимыми на
Тогда если последний член этой последовательности равен нулю, то делится на в противном случае на не делится.
Способ (алгоритм) построения такой последовательности и будет искомым признаком делимости на Математически он может быть описан с помощью функции определяющей каждый следующий член последовательности в зависимости от предыдущего:
удовлетворяющей следующим условиям:
- при значение не определено;
- при значение есть натуральное число;
- если то
- если то и равноделимы на
Если требование равноделимости для всех членов последовательности заменить на более строгое требование равноостаточности, то последний член этой последовательности будет являться остатком от деления на а способ (алгоритм) построения такой последовательности будет признаком равноостаточности на В силу того, что из равенства остатка при делении на нулю следует делимость на , любой признак равноостаточности может применяться как признак делимости. Математически признак равноостаточности тоже может быть описан с помощью функции определяющей каждый следующий член последовательности в зависимости от предыдущего:
удовлетворяющей следующим условиям:
- при значение не определено;
- при значение есть натуральное число;
- если то
- если то и равноостаточны при делении на
Примером такой функции, определяющей признак равноостаточности (и, соответственно, признак делимости), может быть функция
а последовательность, построенная с её помощью будет иметь вид:
По сути применение признака равноостаточности на базе этой функции эквивалентно делению при помощи вычитания.
Другим примером может служить общеизвестный признак делимости (а также равноостаточности) на 10.
Математически этот признак равноостаточности может быть сформулирован следующим образом. Пусть надо выяснить остаток от деления на 10 натурального числа представленного в виде
Тогда остатком от деления на 10 будет . Функция, описывающая это признак равноостаточности будет выглядеть как
Легко доказать, что эта функция удовлетворяет всем перечисленным выше требованиям. Причём последовательность, построенная с её помощью, будет содержать всего один или два члена.
Также легко видеть, что такой признак ориентирован именно на десятичное представление числа — так, например, если применять его на компьютере, использующем двоичную запись числа, то чтобы выяснить , программе пришлось бы сначала поделить на 10.
Для построения признаков равноостаточности и делимости чаще всего используется следующие теоремы:
- При любых целом и натуральном целые числа и равноостаточны при делении на
Пример построения признаков делимости и равноостаточности на 7
Продемонстрируем применение этих теорем на примере признаков делимости и равноостаточности на
Пусть дано целое число
Тогда из первой теоремы полагая будет следовать, что будет равноостаточно при делении на 7 с числом
![]()
Запишем функцию признака равноостаточности в виде:
![]()
И, наконец, остаётся найти такое , при котором для любого выполняется условие В данном случае и функция приобретает окончательный вид:
![]()
А из второй теоремы полагая и взаимно простое с 7, будет следовать, что будет равноделимы на 7 с числом
![]()
Учитывая, что числа и равноделимы на 7, запишем функцию признака делимости в виде:
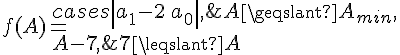
И, наконец, остаётся найти такое , при котором для любого выполняется условие В данном случае и функция приобретает окончательный вид:
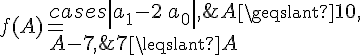
Задачи, которые решаются при помощи действия деления
При помощи операции деления возможно решение не только математических, но и бытовых задач.
К решению математических задач относятся решение примеров с величинами, когда используются понятия деления величин на числа.
К решению бытовых задач относятся различные примеры деления предметов (потенциальных и реальных) между участниками процессов: например, деление обеда на количество членов семьи, деление конфет на число друзей или деление бутылок воды на туристическую группу. Также операция деления может помогать в решении вопросов, касающихся оплаты счетов, банковских операций, совершения покупок в магазинах и т.п.
Признаки делимости — Моя мастерская
При́знак дели́мости —
правило, позволяющее сравнительно быстро определить, является ли число кратным
заранее заданному без необходимости выполнять фактическое деление. Как правило,
основано на действиях с частью цифр из записи числа в позиционной системе
счисления (обычно десятичной).
- Существуют несколько простых правил, позволяющих найти малые
делители числа в десятичной системе счисления: - Признак делимости на 2
- Число делится на 2 тогда и только тогда, когда его последняя
цифра делится на 2, то есть является чётной. - Признак делимости на 3
- Число делится на 3 тогда и только тогда, когда сумма его
цифр делится на 3 (так как все числа вида 10n при делении на 3 дают в остатке
единицу). - Признак делимости на 4
- Число делится на 4 тогда и только тогда, когда число из двух
последних его цифр (оно может быть двузначным, однозначным или нулём) делится
на 4. - Признак делимости на 5
- Число делится на 5 тогда и только тогда, когда последняя
цифра делится на 5 (то есть равна 0 или 5). - Признак делимости на 6
- Число делится на 6 тогда и только тогда, когда оно делится и
на 2, и на 3. - Признак делимости на 7
- Число делится на 7 тогда и только тогда, когда результат
вычитания удвоенной последней цифры из этого числа без последней цифры делится
на 7 (например, 364 делится на 7, так как 36 — (2 × 4) = 28 делится на 7). - Признак делимости на 8
- Число делится на 8 тогда и только тогда, когда три его
последние цифры — нули или образуют число, которое делится на 8. - Признак делимости на 9
- Число делится на 9 тогда и только тогда, когда сумма его
цифр делится на 9. - Признак делимости на 10
- Число делится на 10 тогда и только тогда, когда оно
оканчивается на ноль. - Признак делимости на 11
- Число делится на 11 тогда и только тогда, когда сумма цифр с
чередующимися знаками равна 0 или делится на 11 (то есть 182 919 делится на 11,
так как 1 — 8 + 2 — 9 + 1 — 9 = −22 делится на 11) — следствие факта, что все
числа вида 10n при делении на 11 дают в остатке (-1)n. - Признак делимости на 12
- Число делится на 12 тогда и только тогда, когда оно делится
на 3 и на 4. - Признак делимости на 13
- Число делится на 13 тогда и только тогда, когда число его
десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845
делится на 13, так как 84 + (4 × 5) = 104 делится на 13). - Признак делимости на 14
- Число делится на 14 тогда и только тогда, когда оно делится
на 2 и на 7. - Признак делимости на 15
- Число делится на 15 тогда и только тогда, когда оно делится
на 3 и на 5. - Признак делимости на 17
Число делится на 17 тогда и только тогда, когда число его
десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34.
Поскольку 34 делится на 17, то и 29053 делится на 17).
Признак не всегда
удобен, но имеет определенное значение в математике.
Есть способ немного проще
— число делится на 17 тогда и только тогда, когда разность между числом его
десятков и упятерённым числом единиц кратна 17 (например,
32952→3295-10=3285→328-25=303→30-15=15; поскольку 15 не делится на 17, то и
32952 не делится на 17)
- Признак делимости на 19
- Число делится на 19 тогда и только тогда, когда число его
десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится
на 19, так как 64 + (6 × 2) = 76 делится на 19). - Признак делимости на 23
- Число делится на 23 тогда и только тогда, когда число его
сотен, сложенное с утроенным числом десятков и единиц, кратно 23 (например,
28842 делится на 23, так как 288 + (3 * 42) = 414; продолжаем: 4 + (3 * 14) =
46 — очевидно, делится на 23). - Признак делимости на 25
- Число делится на 25 тогда и только тогда, когда две его последние
цифры делятся на 25 (то есть образуют 00, 25, 50 или 75). - Признак делимости на 99
Разобьем число на группы по 2 цифры справа налево (в самой
левой группе может быть одна цифра) и найдем сумму этих групп, считая их
двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само
число делится на 99.
Признак делимости на 101
Разобьем число на группы по 2 цифры справа налево (в самой
левой группе может быть одна цифра) и найдем сумму этих групп с переменными
знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только
тогда, когда само число делится на 101. Например, 590547 делится на 101, так
как 59-05+47=101 делится на 101).
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
20 : 2 = 10
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Дроби с кратными от 1 до 5
На единицу делится любое целое число.
Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.
Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.

Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.
Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
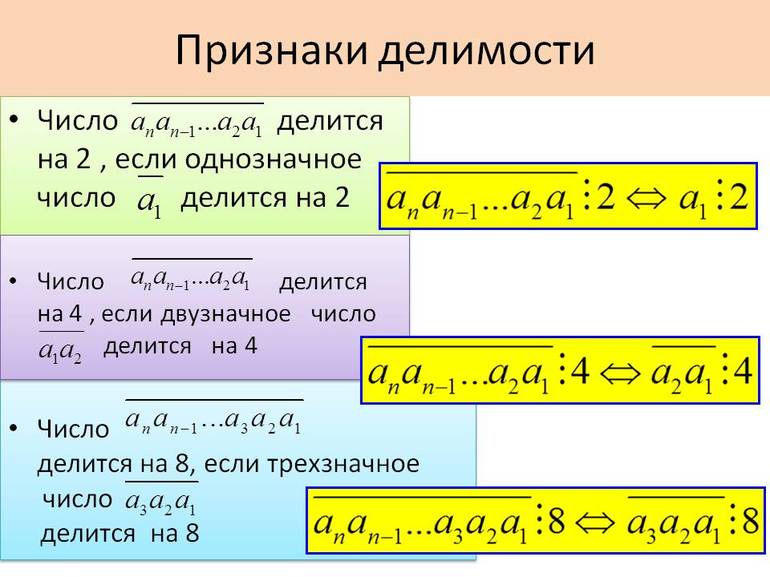
Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.
Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.
Деление методом последовательного вычитания
Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход — деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.
Заголовок
Сколько будет 12 разделить на 4?
Иными словами данную задачу можно сформулировать так: имеется 12 предметов (например, апельсинов), и их нужно разделить на равные группы по 4 предмета (разложить в коробки по 4 штуки). Сколько будет таких групп или коробок по четыре апельсина в каждой?
Шаг за шагом будем отнимать от исходного количества по 4 апельсина и формировать группы по 4 до того момента, пока апельсины не закончатся. Количество шагов, которые нам придется сделать, и будет ответом на изначальный вопрос.
Из 12 апельсинов откладываем первую четверку в коробку. После этого в исходной куче апельсинов остается 12-4=8цитрусовых. Из этих восьми в другую коробку забираем еще 4. Теперь в исходной куче апельсинов осталось 8-4=4штуки. Из этих четырех штук как раз можно сформировать еще одну, отдельную третью коробку, после чего в исходной куче останется 4-4= апельсинов.
Итак, мы получили 3 коробки, по 4 предмета в каждой. Иными словами, мы разделили 12 на 4, и получили в результате 3.
Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.
Важно!
При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.
Для закрепления рассмотрим еще один, более сложный пример.
Пример 1. Деление последовательным вычитанием
Вычислим результат деления числа 108 на 27 методом последовательного вычитания.
Первое действие: 108-27=81.
Второе действие: 81-27=54.
Третье действие: 54-27=27.
Четвертое действие: 27-27=.
Более действий не требуется. Мы получили ответ:
108÷27=4
Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.
Общие сведения
Операция деления одного числа на другое является довольно сложной, поскольку она классифицируется на два направления в зависимости от частного:
- Целочисленное.
- Дробное.
В первом случае частное, или результат операции деления, является целым числом, т. е. получается без остатка. Об этом говорят, что деление выполнено нацело. Очень часто подбор делителя осуществляется при сокращении дробных выражений по свойству обыкновенной дроби.

Однако не всегда можно поделить одну величину на другую нацело. В этом случае частное представляется в виде дробного тождества.
Дробные величины
Дробное выражение может записываться в десятичной, обыкновенной и смешанной формах. Обыкновенное дробное выражение — незаконченная операция деления, поскольку в нем существуют только два компонента, а именно:
- Делимое (значение, делящееся на некоторую величину и представляющее какое-либо целое значение или его часть).
- Делитель (величина, показывающая количество равных частей, на которые требуется разделить искомый элемент-делимое).
Записывается обыкновенная дробь следующим образом: m/n, а читается так: «эм энных» (2/5 — две пятых). Элемент «m» еще называют числителем, а «n» — знаменателем. Разделяются эти два компонента при помощи косой черты. Последняя обозначает символ операции деления кроме стандартного двоеточия «:».
Следует отметить, что десятичное дробное тождество является частным, или результатом деления числителя на знаменатель. Далее необходимо подробно рассмотреть для общего развития преобразование неправильного дробного тождества в смешанное число.
Смешанное число
Смешанная форма представления состоит из целой части и правильной обыкновенной дроби. Записывается следующим образом: R[P/S], где R — целая часть, P — числитель и S — знаменатель. Следует отметить, что смешанное число всегда получается из неправильной дроби. У последней числитель всегда больше знаменателя.
Специалисты предлагают простую методику преобразования дробного выражения неправильного типа в смешанную форму. Она выглядит следующим образом:
- Записать выражение: m/n, где m>n.
- Выделить целую часть: m/n=P.
- Произвести расчет нового числителя m’ по формуле: m’=m-P*n.
- Результат: Р[m’/n].
Далее требуется разобрать применение методики на практике. Реализация алгоритма имеет такой вид:
- Искомая неправильная дробь: 63/11.
- Целая часть: 5.
- Новый числитель: m’=63−5*11=8.
- Результат: 5[8/11].
Обратный алгоритм преобразования числа смешанной формы в неправильную обыкновенную дробь осуществляется в такой последовательности:
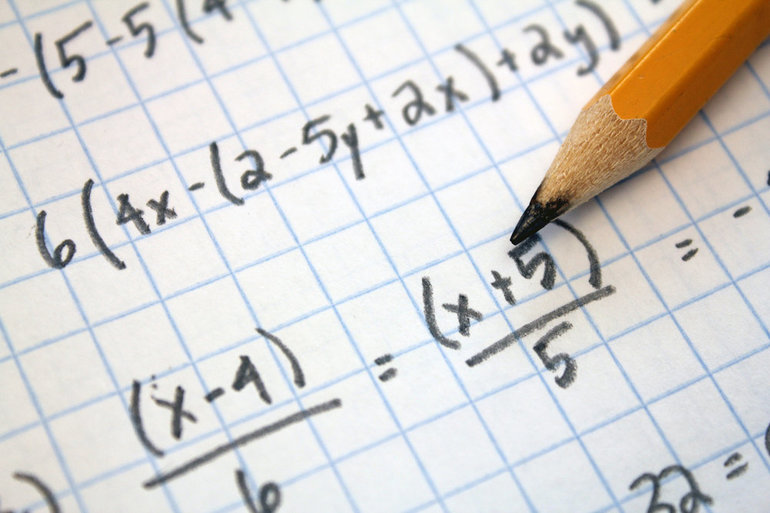
- Пишется величина: Р[m’/n].
- Рассчитывается новое значение числителя для неправильной дроби: m=nP+m’.
- Записывается результат: m/n.
Для проверки работоспособности методики нужно рассмотреть пример. Реализация алгоритма выглядит таким образом:
- Записать величину: 5[8/11].
- Числитель: m=11*5+8=63.
- Смешанное число: 63/11.
Однако перед тем как перейти к критериям делимости, необходимо разобрать следующие термины: разрядная сетка и цифра.
Структура числа
Число состоит из разрядной сетки, т. е. позиции, в состав которой входят определенные компоненты — цифры (математические символы для построения числовых выражений). Каждая из них стоит на некотором месте. От последнего зависит величина числа. Для примера нужно разобрать величину «45681». Ее необходимо расписать по элементам-разрядам:
- Единицы: 1.
- Десятки: 8.
- Сотни: 6.
- Тысячи: 5.
- Десятитысячи: 4.
Все пять пунктов являются разрядной сеткой, элементы которой имеют определенное числовое значение. Из последних и складывается величина, т. е. 1*1+10*8+100*6+1000*5+10000*4=45681. Числа бывают четными и нечетными. Четное — величина, заканчивающаяся на одну из цифр {0;2;4;6;8}. Все остальные значения считаются нечетными.
Кроме того, любая величина может быть простой и составной. Первую невозможно разделить на какое-либо число, кроме единицы и самого себя. Для примера можно рассмотреть «7».
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1
Теперь раскладываем число 12 на простые множители:
Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
2 × 2 = 4
Занесём число 4 в нашу таблицу делителей
Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:
Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:
Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
- записать в качестве первого делителя единицу;
- разложить исходное число на простые множители и выписать из полученных простых множителей те множители, которые являются делителями исходного числа (если множитель повторяется, то выписать его нужно только один раз);
- найти все возможные произведения полученных простых множителей между собой. Получаемые в результате ответы будут остальными делителями исходного числа.
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
1
Теперь разложим число 6 на простые множители:
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
Теперь найдём все возможные произведения простых множителей числа 6. В данном случае имеется только одно произведение, а именно 2 × 3. Это произведение равно 6. Допишем число 6 к нашим делителям:
1, 2, 3, 6
Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.
Задания для самостоятельного решения
Задание 1. Разложите число 256 на простые множители
Решение:
Задание 2. Разложите число 52 на простые множители
Решение:
Задание 3. Разложите число 98 на простые множители
Решение:
Задание 4. Разложите число 116 на простые множители
Решение:
Задание 5. Разложите число 228 на простые множители
Решение:
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Распределительные свойства деления
К распределительным свойствам деления относятся операции:
- деление суммы на число;
- деление разности на число;
- деление произведения на число;
- деление числа на произведение.
При делении суммы на число необходимо каждое из слагаемых поделить на число, а потом сложить результаты частных.
При делении разности на число необходимо также каждое из чисел примера поделить на делитель, но при этом нужно соблюдать строгую последовательность. Сначала необходимо провести деление уменьшаемого, потом — вычитаемого, и только после этого провести операцию вычитания.
Деление произведения на число подразумевает деление только одного из сомножителей и дальнейшее умножение без изменений. Выбор множителя зависит от величины делителя и удобности проведения операции деления.
Смысл данного правила заключается в том, что при делении произведения его результат уменьшается в количество раз, определяемое делителем. Если любой из множителей произведения уменьшить в данное количество раз, результат произведения также автоматически уменьшится во столько же раз.
Деление числа на произведение требует проведение операций деления в строгом порядке. Для решения примера потребуется деление первого сомножителя, деление результата на второй сомножитель, третий и так далее.













![Делимость на 11 [1967 перельман я.и. - занимательная алгебра]](http://ieducations.ru/wp-content/uploads/2/b/4/2b410da5244b92e017972c97e3074f2e.jpeg)






![Признаки-делимости [сайт патологического холостяка]](http://ieducations.ru/wp-content/uploads/6/d/6/6d617b79b86f50327212211db15f6cef.jpeg)













