Дроби и действия с дробями

Задачи на скорость, время, расстояние

Пример 1

За 7 часов теплоход проделал путь в 210 км. Поезд за 4 часа преодолел 420 км. Во сколько раз скорость поезда больше скорости теплохода?

Решение

Записываем краткое условие. В этом типе задач оно немного отличается от стандартного;
У нас есть два объекта — теплоход и поезд. Это значит, что в таблице будет две строки;
Для каждого объекта есть три значения, соответственно, и столбцов будет три;
Заполняем числами таблицу. Что должно получится смотрите ниже;

Таблица 3 — Краткое условие

	Скорость	Время	Расстояние
Теплоход	?	7	210
Поезд	?	3	360

Приступим к поиску неизвестных. Нам нужно узнать скорость у теплохода и поезда. Для этого используется формула — скорость равна результату деления расстояния на время. Математически записывается так — V=S:T;
Подставив числа из условия, получаем выражение для скорости теплохода. 210:7=30 км/ч;
Также поступаем и для расчёта скорости поезда. 360:3=120 км/ч;
Мы нашли все неизвестные и теперь возвращаемся к главному вопросу задачи. Нам нужно определить во сколько раз скорость поезда превышает скорость теплохода;
Для этого делим большее значение на меньшее. Получается: 120:30=4;
В ответ пишем, что скорость теплохода и поезда отличается в 4 раза.

Пример 2

Автомобилист за 4 часа проехал 320 километров. Какой путь проделает автомобиль за 8 часов с той же скоростью?

Решение

Записываем краткое условие. Объект один, значит строка будет одна. Столбцов стандартно три;
Заполняем числа из условия в таблицу. Что получится смотрите ниже;

Таблица 4 — краткое условие

	Скорость	Время	Расстояние
Автомобиль	?	4	320

Ищем неизвестные. В нашем случае нужно найти скорость. Для этого воспользуемся формулой V=S:T. Подставляем числа и получаем: 320:4=80 км/ч;
После того, как стали известны все значения, переходим к главному вопросу задачи — сколько проедет автобус за 8 часов с той же скоростью;
Для расчёта используем формулу S=VT. Подставляем числа и получаем: 80×8=640 км;
Записываем полученное значение в ответ к задаче.

Решение этих задач требует знать основную формулу S=VT. Расшифровывается она так: расстояние равно произведению скорости на время. Из неё вытекают все решения для нахождения неизвестных. Также для упрощения задачи можно рисовать схему.

Сложение дробей с одинаковыми знаменателями

Сложение дробей бывает двух видов:

Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.

Например, слóжим дроби

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к

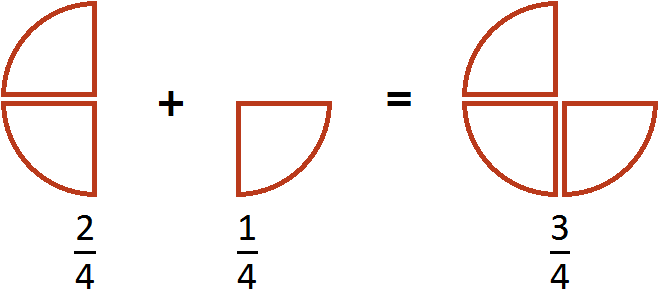
Пример 2. Сложить дроби

Опять же складываем числители, а знаменатель оставляем без изменения:

В ответе получилась неправильная дробь

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к

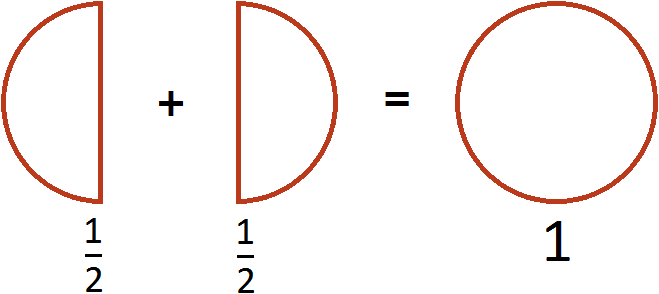
Пример 3. Сложить дроби

Опять же складываем числители, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к

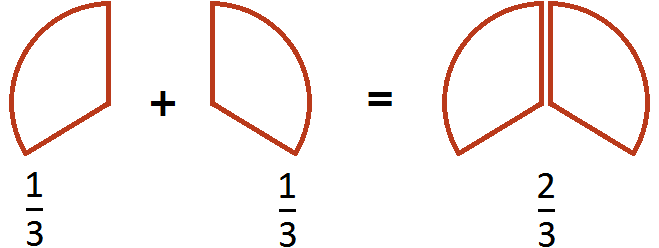
Пример 4. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:

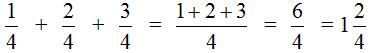
Попробуем изобразить наше решение с помощью рисунка. Если к

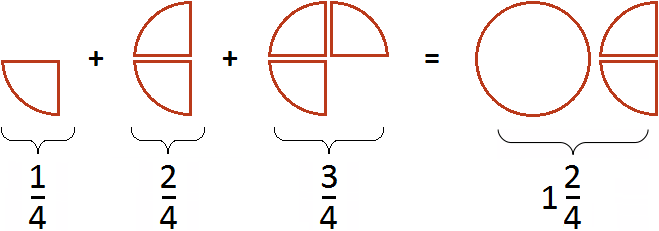
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:

Нахождение числа по его дроби

Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:

Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.

Задача 1. Потратили 50 рублей, это составило от первоначальной суммы. Найдите первоначальную сумму денег.

Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:

50 · 6 = 300 (р.).

Ответ: Первоначальная сумма — 300 рублей.

Задача 2. Потратили 600 рублей, это составило от первоначальной суммы денег. Найдите первоначальную сумму.

Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):

600 : 2 · 3 = 900 (р.).

Ответ: Первоначальная сумма — 900 рублей.

Второй способ нахождения целого по его части:

Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.

Задача 3. Отрезок AB, равный 42 см, составляет длины отрезка CD. Найти длину отрезка CD.

Решение:

Ответ: Длина отрезка CD 70 см.

Задача 4. В магазин привезли арбузы. До обеда магазин продал , после обеда — привезённых арбузов, и осталось продать 80 арбузов. Сколько всего арбузов привезли в магазин?

Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):

Итак, мы узнали, что 80 арбузов составляет от общего количества привезённых арбузов. Теперь узнаем сколько арбузов от общего количества составляет , а затем сколько арбузов составляют (количество привезённых арбузов):

2) 80 : 4 · 15 = 300 (арбузов).

Ответ: Всего в магазин привезли 300 арбузов.

Примеры сложения и вычитания дробей с переменными

Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 6

Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.

Решение

Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2. После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
Сложение было выполнено. Видно, что можно произвести сокращение дроби. Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2из формул сокращенного умножения. Тогда получаем, чтоlg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x
Заданные дроби вида x-1x-1+xx+1 с разными знаменателями. После преобразования можно перейти к сложению.

Рассмотрим двоякий способ решения.

Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида

x-1x-1=x-1(x-1)·x+1=1x+1

Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.

В таком случае необходимо избавляться от иррациональности в знаменателе.

Получим:

1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1

Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда

x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1

Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.

В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.

Пример 7

Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x

Решение

Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться произведение вида x5·ln2x+1·2x-4. Отсюда x4является дополнительным множителем к первой дроби, а ln(x+1)ко второй. После чего производим вычитание и получаем, что:x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)
Данный пример имеет смысл при работе со знаменателями дробями. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.

После чего получаем, что

1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2

Ответ:

1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.

Два подхода к решению заданий с разными числами

В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.

В первом подходе смешанное число будет представлено в виде неправильной дроби.

После выполнения действий, описанных выше, получится такое значение: 13/5.

Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.

При нахождении разности эти же числа вычитаются: 143 — 70 = 73. Ответом будет дробь: 73/55.

При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.

Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5 : 14/11 = 13/5 х 11/14 = 143/70.

Во втором подходе неправильная дробь обращается в смешанное число.

После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.

Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.

При вычитании знак «+» заменяется на «-». 2 — 1 = 1, 33/55 — 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.

Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.

Более быстрый способ

В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:

Посчитать, сколько цифр стоит после запятой. Например, у дроби 1,75 таких цифр две, а у 0,0025 — четыре. Обозначим это количество буквой $n$.
Переписать исходное число в виде дроби вида $\frac{a}{{{10}^{n}}}$, где $a$ — это все цифры исходной дроби (без «стартовых» нулей слева, если они есть), а $n$ — то самое количество цифр после запятой, которое мы посчитали на первом шаге. Другими словами, необходимо разделить цифры исходной дроби на единицу с $n$ нулями.
По возможности сократить полученную дробь.

Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:

Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому $n=2$. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64. Переходим ко второму шагу: ${{10}^{n}}={{10}^{2}}=100$, поэтому в знаменателе стоит именно сто. Ну а затем остаётся лишь сократить числитель и знаменатель.:)

Ещё один пример:

Здесь всё чуть сложнее. Во-первых, цифр после запятой уже 3 штуки, т.е. $n=3$, поэтому делить придётся на ${{10}^{n}}={{10}^{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.

Наконец, последний пример:

Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.

§ Как правильно заниматься дома

Для того чтобы занятия действительно приносили пользу, необходимо придерживаться определенных правил, которые помогут сделать день продуктивнее, без утомления ребенка:

Самое главное правило, которое пригодиться не только школьнику, но и любому взрослому человеку, это правильное чередования умственного труда и физического. Необходимо составить распорядок дня так, чтобы после физических нагрузок обязательно шли более спокойные, умственные занятия

Нельзя делать уроки сразу же после возвращения из школы, то же самое касается и дополнительных занятий.
Для решения задач вне школьной программы лучше всего выбирать менее загруженные уроками дни.
Во время занятий нужно убрать все отвлекающие факторы, для того чтобы внимание ребенка не рассеивалось. Если есть возможность решить важные дела перед уроками, то лучше сделать это заранее.
Начинать всегда нужно со сложных задач, а затем переходить к более простым.
Обязательно нужно хвалить ребенка за его достижения и правильно выполненную работу.
Для того чтобы мозг работал, детям нужно давать шанс самостоятельно решать примеры и задачи

Даже если в течение долгого времени он не может найти ответ, не нужно делать очевидных подсказок, пусть он найдет путь решения самостоятельно.
Хорошо запоминать принцип математических решений помогают ассоциации, например, дроби можно представлять как кусочки одного торта или яблока.

Деление смешанных чисел

Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.

Деление смешанного числа на смешанное число

Запоминаем
Чтобы разделить одно смешанное число на другое, переведите оба числа в неправильные дроби и выполните деление, следуя правилу деления дробей.

Пример. Найдите результат деления смешанного числа на смешанное число

Как решаем:

Запишем выражение:

Следуя правилу, переведем оба смешанных числа в неправильные дроби.

Пользуясь правилом деления дробей, находим частное:

Ответ: .

Деление смешанного числа на целое число

Запоминаем
Чтобы разделить смешанное число на целое число, переведите смешанное число в неправильную дробь и выполните деление.

Пример. Разделите смешанное число на натуральное число 15

Как решаем:

Запишем выражение

Следуя правилу, переведем смешанное число в неправильную дробь

Выполним деление

Ответ: .

Деление целого числа на смешанное число

Запоминаем
Чтобы разделить целое число на смешанное число, переведите смешанное число в неправильную дробь и выполните деление.

Пример. Выполните деление натурального числа 30 на смешанное число

Запишем выражение

Представим смешанное число в виде неправильной дроби .

Выполним деление .

Выделим из полученной неправильной дроби целую часть .

Ответ: .

Деление смешанного числа на обыкновенную дробь

Запоминаем
Чтобы разделить смешанное число на обыкновенную дробь, представьте смешанное число в виде неправильной дроби и выполните деление.

Пример. Разделите смешанное число на обыкновенную дробь

Как решаем:

Запишем выражение .

Представим смешанное число в виде неправильной дроби .

Выполним деление, следуя правилу деления дробей: .

Ответ: .

Обратные числа

Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».

Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.

Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:

Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.

Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:

Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь

Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:

Значит обратным к числу 5, является число

Обратное число можно найти также для любого другого целого числа.

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.

§ 3адания на тему «Умножение и деление десятичных дробей»

3адание 1

Выполнить действия:

5,6 • 8,34;
11,4 • 24,08;
0,56 • 34,9;
6,8 : 3,2;
33,021 : 12,23;
59,72 : 6,26.

Ответ: 1) 46,704; 2) 274,512; 3) 19,544; 4) 2,125; 5) 2,7; 6) 9,54.

3адание 2

3агадано число, если его увеличить в 3 раза, а затем прибавить 2,16, то получиться 27,96. Какое число было загадано?

Решение: Пусть неизвестное число будет x, тогда можно составить уравнение х • 3 + 2,16 = 27,96.

1 действие:

х • 3 + 2,16 = 27,96;

3х = 27,96 — 2,16;

3х = 25,8;

х = 25,8 : 3;

х = 8,6.

Ответ: было загадано число 8,6.

3адание 3

Расстояние между населенными пунктами равно 53,7 км. Навстречу друг другу вышли два пешехода, скорость первого 3,8 км/ч, второго — 4,6 км/ч. Какое расстояние будет между ними через 2,7 часа?

Решение: Нужно вычислить, какое расстояние пешеходы пройдут за 2,7 часа.

1 действие: 3,8 • 2,7 = 10,26 (км) — пройдет первый пешеход.

2 действие: 4,6 • 2,7 = 12,42 (км) — пройдет второй пешеход.

После того как стало известно, сколько прошли пешеходы, можно высчитать, какой путь им еще нужно преодолеть до встречи друг с другом.

3 действие: 53,5 — 10,26 — 12,42 = 30,82 (км).

Ответ: через 2,7 часа между пешеходами будет 30,82 км.

СКАЧАТЬ И РАСПЕЧАТАТЬ ОТДЕЛЬНО ФАЙЛ «ЗАДАНИЯ ПО МАТЕМАТИКЕ 5 КЛАСС: ДЛЯ ЗАНЯТИЙ ДОМА (БЕЗ ОТВЕТОВ) В ФОРМАТЕ PDF

СКАЧАТЬ И РАСПЕЧАТАТЬ ОТДЕЛЬНО ФАЙЛ «ЗАДАНИЯ ПО МАТЕМАТИКЕ 5 КЛАСС: ДЛЯ ЗАНЯТИЙ ДОМА (ОТВЕТЫ) В ФОРМАТЕ PDF

Примеры с десятичными дробями 5 класс с объяснением

Много вопросов у детей вызывают примеры на несколько действий. Разберем пару таких примеров.

Пример 1.

( 0,4 · 8,25 — 2,025 ) : 0,5 =

Второе действие находится там же в скобках, это разность. От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.

Третье действие-деление. Полученную разность во втором действии делим на 0,5. Запятая переносится на один знак. Результат 2,55.

Ответ: 2,55.

Пример 2.

( 0, 93 + 0, 07 ) : ( 0, 93 — 0, 805 ) =

Первое действие сумма в скобках.Складываем в столбик, помним, что запятая под запятой. Получаем ответ 1,00.

Второе действие разность из второй скобки. Так как у уменьшаемого меньше знаков после запятой, чем у вычитаемого, добавляем недостающий. Результат вычитания 0 ,125.

Третьим действие делим сумму на разность. Запятая переносится на три знака. Получилось деление 1000 на 125.

Ответ: 8.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

Это выражение можно прочитать по-разному:

В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.

Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

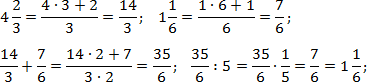
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

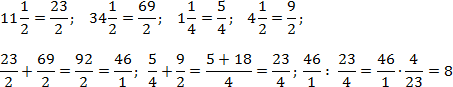
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

Умножение и деление дробей
Тест к уроку «Сложные выражения с дробями» (легкий)
Тест к уроку «Округление с избытком и недостатком» (1 вариант)
Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
Формула простого процента: как найти исходное значение
Сложная задача B14 на смеси и сплавы

Арифметические вычисления. Проценты. Обыкновенные дроби. Действия над обыкновенными дробями.

1º. Натуральные числа – это числа, употребляемые при счете. Множество всех натуральных чисел обозначают N, т.е. N = (1, 2, 3, …).

Дробью называется число, состоящее из нескольких долей единицы. Обыкновенной дробью называется число вида , где натуральное число n показывает, на сколько равных частей разделена единица, а натуральное число m показывает, сколько таких равных частей взято. Числа m и n называют соответственно числителем и знаменателем дроби.

Если числитель меньше знаменателя, то обыкновенная дробь называется правильной; если числитель равен знаменателю или больше него, то дробь называется неправильной. Число, состоящее из целой и дробной частей, называется смешанным числом.

Например, — правильные обыкновенные дроби, — неправильные обыкновенные дроби, 1 — смешанное число.

2º. При выполнении действий над обыкновенными дробями следует помнить следующие правила:

1) Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.

Например, а) ; б) .

Деление числителя и знаменателя дроби на их общий делитель, отличный от единицы, называется сокращением дроби.

2) Чтобы смешанное число представить в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, записать полученную сумму числителем дроби, а знаменатель оставить прежним.

Аналогично любое натуральное число можно записать в виде неправильной дроби с любым знаменателем.

Например, а) , так как ; б) и т.д.

3) Чтобы неправильную дробь записать в виде смешанного числа (т.е. из неправильной дроби выделить целую часть), нужно числитель разделить на знаменатель, частное от деления взять в качестве целой части, остаток — в качестве числителя, знаменатель оставить прежним.

Например, а) , так как 200 : 7 = 28 (ост. 4); б) , так как 20 : 5 = 4 (ост. 0).

4) Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное (НОК) знаменателей этих дробей (оно и будет их наименьшим общим знаменателем), разделить наименьший общий знаменатель на знаменатели данных дробей (т.е. найти дополнительные множители для дробей), умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Например, приведем дроби к наименьшему общему знаменателю:

, , ;

;

630 : 18 = 35, 630 : 10 = 63, 630 : 21 = 30.

Значит, ; ; .

5) Правила арифметических действий над обыкновенными дробями:

a) Сложение и вычитание дробей с одинаковыми знаменателями выполняется по правилу:

b) Сложение и вычитание дробей с разными знаменателями выполняется по правилу a), предварительно приведя дроби к наименьшему общему знаменателю.

c) При сложении и вычитании смешанных чисел можно обратить их в неправильные дроби, а затем выполнить действия по правилам a) и b),

d) При умножении дробей пользуются правилом:

e) Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

f) При умножении и делении смешанных чисел, их предварительно переводят в неправильные дроби, а затем пользуются правилами d) и e).

3º. При решении примеров на все действия с дробями следует помнить, что сначала выполняются действия в скобках. Как в скобках, так и вне их сначала выполняют умножение и деление, а затем сложение и вычитание.

Рассмотрим выполнение вышеизложенных правил на примере.

Пример 1. Вычислить: .

1) ;

2) ;

3) ;

4) ;

5) . Ответ: 3.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9460 — | 7447 — или читать все.

78.85.5.224 studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock! и обновите страницу (F5)очень нужно

Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.

Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.

Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.