Правило сложения дисперсий
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).
Общая дисперсия характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
- — групповые средние,
- — численность единиц i-й группы
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— дисперсия i-ой группы.
Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()
Эмпирический коэффициент детерминации () характеризует долю межгрупоовой дисперсии в общей дисперсии:
и показывает насколько вариация признака в совокупности обусловлена фактором группировки.
Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }
оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениями являются нуль и единица. Чем ближе к единице, тем теснее связь.
Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:
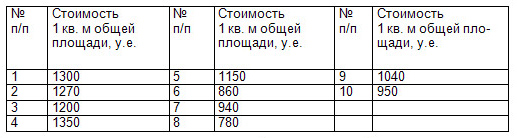
При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.
Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади: Общую дисперсию определим по формуле:
.
Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:
а) для домов, построенных вблизи центра:
б) для домов, построенных далеко от центра:
Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии:
Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии
Найденные дисперссии в сумме дают величину общей дисперсии
Эмпирический коэффициент детерминации:
показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81,8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18,2% — другими факторами.
Эмприческое корреляционное отношение свидетельствует о существенном влиянии на стоимость жилья месторасположения домов.
Правило сложения дисперсий для доли признака записывается так:
а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:
общая дисперсия:

Формулы межгрупповой и внутригрупповой дисперсий:
Другие статьи по данной теме:
- назад: Средние величины в статистике: сущность, свойства, виды. Примеры решения задач
- далее: Выборочное наблюдение: понятие, виды, ошибки выборки, оценка
результатов. Примеры решения задач
Список использованных источников
- Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями.
Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001; - Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики,
информатики, финансов и права. — М., 2003; - Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
- Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика»
для студентов экономических специальностей: УрГЭУ, 2007;
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
Принципы определения показателей вариации
Пример №4
Средние величины и показатели вариации имеют в статистике важное значение. Они широко применяются для характеристики статистических совокупностей по варьирующим признакам.
В задачах контрольных работ могут приводиться так называемые открытые интервалы, то есть, интервалы, у которых верхняя или нижняя границы точно не определены, а сама граница остается как бы открытой
В этом случае за величину открытого интервала условно принимается величина смежного закрытого интервала. Например, дан вариационный ряд распределения работников магазина:
| Группы работающих по величине заработка (руб. в месяц) | Число работающих (чел.) |
| до 8000 | 6 |
| от 8000 до 9000 | 10 |
| от 9000 до 10000 | 14 |
| и т.д. |
определении среднего квадратического отклоненияix
Примеры решения задач по теме «Показатели вариации в статистике»
Задача 1. При изучении влияния рекламы на размер среднемесячного вклада в банках района
обследовано 2 банка. Получены следующие результаты:
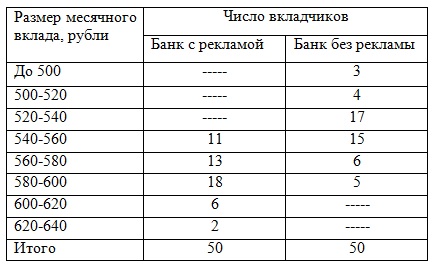 |
Определить:
1) для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада;
2) средний размер вклада за месяц для двух банков вместе;
3) Дисперсию вклада для 2-х банков, зависящую от рекламы;
4) Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы;
5) Общую дисперсию используя правило сложения;
6) Коэффициент детерминации;
7) Корреляционное отношение.
Решение
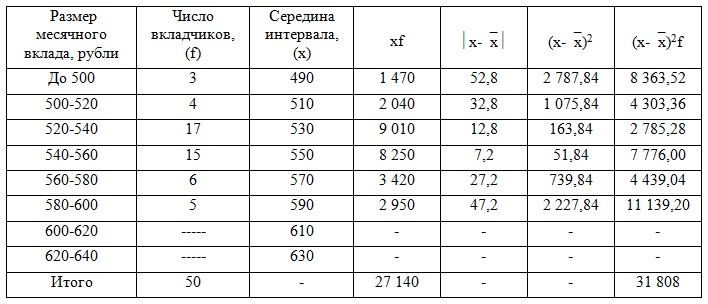
1) Составим расчетную таблицу для банка с рекламой. Для определения среднего размера
вклада за месяц найдем середины интервалов. При этом величина открытого интервала (первого) условно
приравнивается к величине интервала, примыкающего к нему (второго).
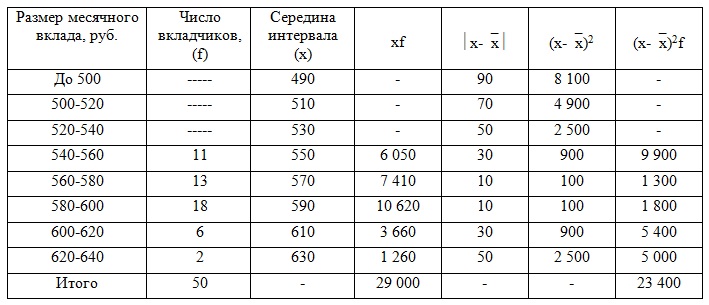 |
Средний размер вклада найдем по формуле средней арифметической взвешенной:
= 29 000/50 = 580 руб.
Дисперсию вклада найдем по формуле:
= 23 400/50 = 468
Аналогичные действия произведем для банка без рекламы:
 |
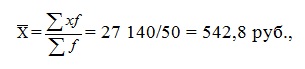 |
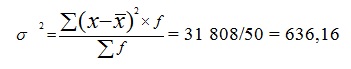 |
2) Найдем средний размер вклада для двух банков вместе. Хср =(580×50+542,8×50)/100 = 561,4 руб.
3) Дисперсию вклада, для двух банков, зависящую от рекламы найдем по формуле: σ2=pq (формула
дисперсии альтернативного признака). Здесь р=0,5 – доля факторов, зависящих от рекламы; q=1-0,5,
тогда σ2=0,5*0,5=0,25.
4) Поскольку доля остальных факторов равна 0,5, то дисперсия вклада для двух банков, зависящая от всех факторов
кроме рекламы тоже 0,25.
5) Определим общую дисперсию, используя правило сложения.
= (468*50+636,16*50)/100=552,08
= / 100= 34 596/ 100=345,96
σ2 = σ2факт + σ2ост = 552,08+345,96 = 898,04
6) Коэффициент детерминации η2 = σ2факт / σ2 =
345,96/898,04 = 0,39 = 39% — размер вклада на 39% зависит от рекламы.
7) Эмпирическое корреляционное отношение η = √η2 = √0,39 = 0,62 – связь достаточно тесная.
Задача 2. Имеется группировка предприятий по величине товарной продукции:
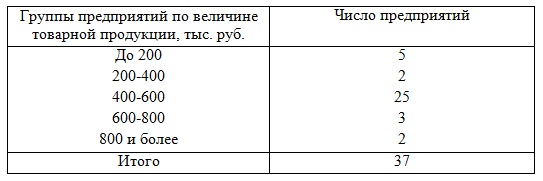 |
Определить: 1) дисперсию величины товарной продукции; 2) среднее квадратическое отклонение; 3) коэффициент
вариации.
Решение
1) По условию представлен интервальный ряд распределения. Его необходимо выразить дискретно, то есть найти середину
интервала (х’). В группах закрытых интервалов середину найдем по простой средней арифметической. В группах с
верхней границей — как разность между этой верхней границей и половиной размера следующего за ним интервала
(200-(400-200):2=100).
В группах с нижней границей – суммой этой нижней границы и половины размера предыдущего интервала
(800+(800-600):2=900).
Расчет средней величины товарной продукции делаем по формуле:
Хср = k×((Σ((х’-a):k)×f):Σf)+a. Здесь а=500 — размер варианта при наибольшей частоте, k=600-400=200 — размер
интервала при наибольшей частоте. Результат поместим в таблицу:
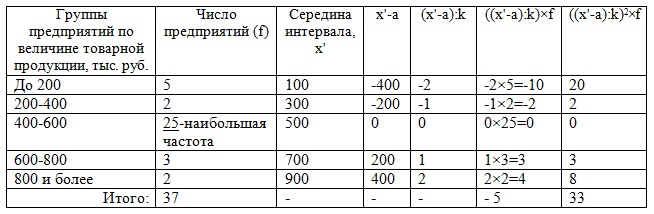 |
Итак, средняя величина товарной продукции за изучаемый период в целом равна Хср = (-5:37)×200+500=472,97 тыс. руб.
2) Дисперсию найдем по следующей формуле:
σ2 = (33/37)*2002-(472,97-500)2 = 35 675,67-730,62 = 34 945,05
3) среднее квадратическое отклонение: σ = ±√σ2 = ±√34 945,05 ≈ ±186,94 тыс. руб.
4) коэффициент вариации: V = (σ /Хср)*100 = (186,94 / 472,97)*100 = 39,52%
Понятие вариации
Вариация определяет различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период (момент времени). Причиной вариации бывают разные условия существования разных единиц совокупности. Например, даже близнецы в процессе жизни приобретают различия в росте, весе, а также в таких признаках, как уровень образования, доход, количество детей и т.д.
Вариация возникает в результате того, что сами значения признака складываются под суммарным влиянием разнообразных условий, которые разным образом сочетаются в каждом отдельном случае. Таким образом, величина любого варианта объективна.
Вариация характерна всем без исключения явлениям природы и общества, кроме законодательно закрепленных нормативных значений отдельных социальных признаков. Исследования вариации в статистике имеют огромное значение, помогают познать сущность изучаемого явления. Нахождение вариации, выяснение ее причин, выявление влияния отдельных факторов дают важную информацию для внедрения научно обоснованных управленческих решений.
Средняя величина дает обобщенную характеристику признака совокупности, но она не раскрывает её строения. Среднее значение не показывает, как располагаются вокруг нее варианты осредненного признака, распределены ли они вблизи средней или отклоняются от нее. Средняя в двух совокупностях может быть одинаковой, но в одном варианте все индивидуальные значения отличаются от нее незначительно, а в другом — эти отличия велики, т.е
в первом случае вариация признака мала, а во втором — велика, это имеет очень важное значение для характеристики значимости средней величины
Для того, чтобы руководитель организации, управляющий, научный работник могли изучать вариацию и управлять ей, статистикой разработаны специальные методы исследования вариации (система показателей). С их помощью вариация находится, характеризуются ее свойства. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации.
Вариационный ряд и его формы
Вариационный ряд — это упорядоченное распределение единиц совокупности чаще по возрастающим (реже убывающим) значениям признака и подсчет числа единиц с тем или иным значением признака. Когда численность единиц совокупности большая, ранжированный ряд становится громоздким, его построение занимает длительное время. В такой ситуации вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.
Существуют следующие формы вариационного ряда:
- Ранжированный ряд представляет собой, перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
- Дискретный вариационный ряд — это таблица, состоящая из двух строк или граф: конкретных значений варьирующего признака х и числа единиц совокупности с данным значение f — признака частот. Он строится тогда, когда признак принимает наибольшее число значений.
- Интервальный ряд.
Размах вариации
Размах вариации определяется как абсолютная величина разности между максимальными и минимальными значениями (вариантами) признака:
Размах вариации показывает только крайние отклонения признака и не отражает отдельных отклонений всех вариантов в ряду. Он характеризует пределы изменения варьирующего признака и зависим от колебаний двух крайних вариантов и абсолютно не связан с частотами в вариационном ряду, т. е. с характером распределения, что придает этой величине, случайный характер. Для анализа вариации нужен показатель, который отражает все колебания вариационного признака и даёт общую характеристику. Простейший показатель такого вида — среднее линейное отклонение.


































