Сила упругости. закон гука

1.12. Сила упругости. Закон Гука window.top.document.title = «1.12. Сила упругости. Закон Гука»;

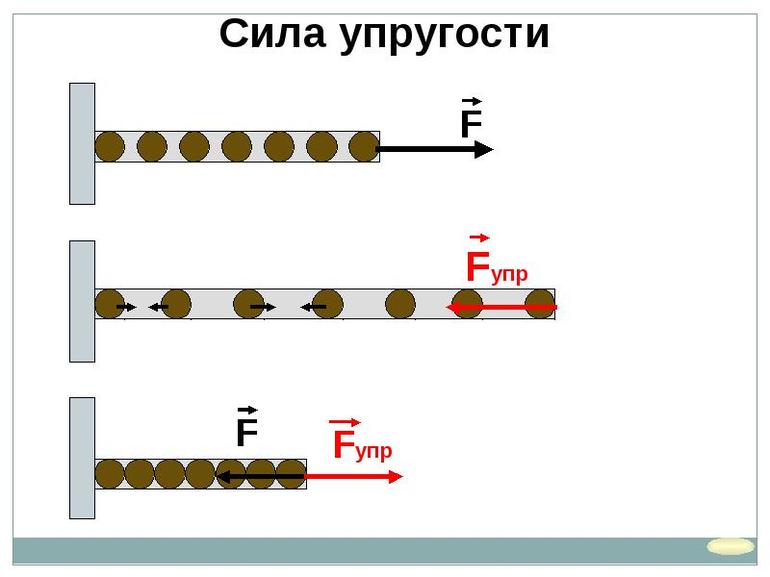
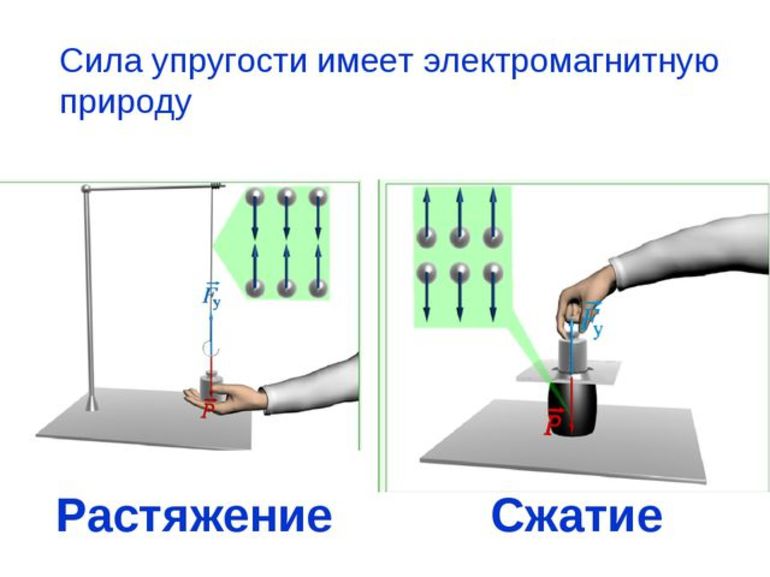
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

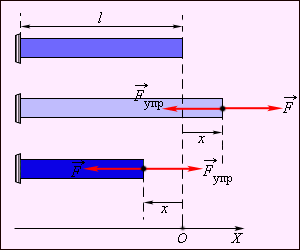Рисунок 1.12.1.Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –F_упр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.

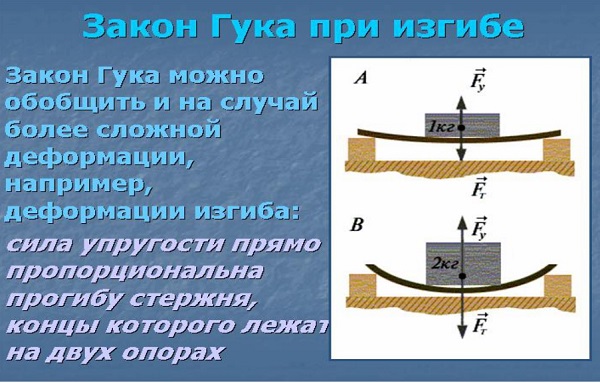
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).

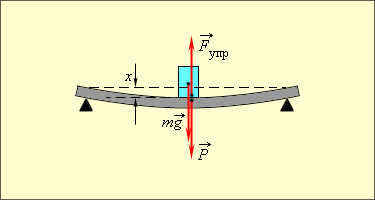Рисунок 1.12.2.Деформация изгиба.

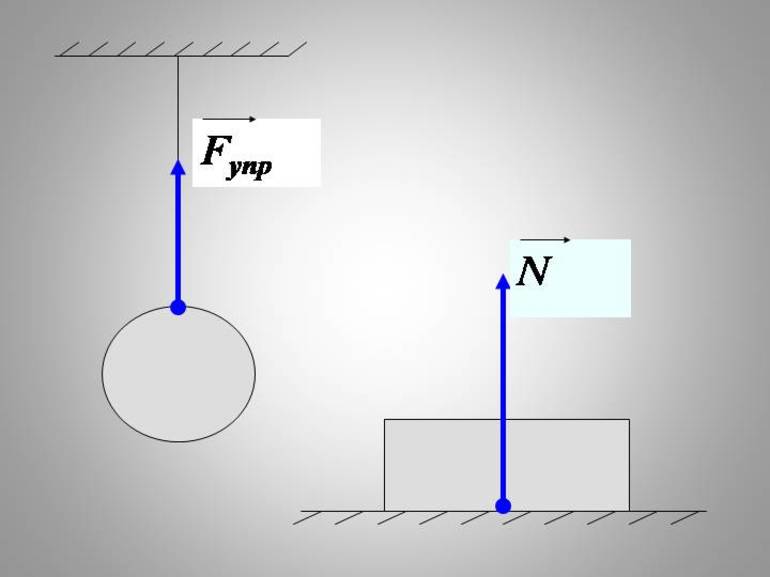
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется .

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.

Рисунок 1.12.3.Деформация растяжения пружины.

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

Модель. Закон Гука

Коэффициент упругости

Коэффицие́нт упру́гости (иногда называют коэффициентом Гука, коэффициентом жёсткости или жёсткостью пружины) — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу упругости. Применяется в механике твердого тела в разделе упругости. Обозначается буквой k, иногда D или c. Имеет размерность Н/м или кг/с2 (в СИ), дин/см или г/с2 (в СГС).

Коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина изменилась на единицу расстояния.

Определение и свойства

Коэффициент упругости по определению равен силе упругости, делённой на изменение длины пружины: k = F e / Δ l . {\displaystyle k=F_{\mathrm {e} }/\Delta l.} Коэффициент упругости зависит как от свойств материала, так и от размеров упругого тела. Так, для упругого стержня можно выделить зависимость от размеров стержня (площади поперечного сечения S {\displaystyle S} и длины L {\displaystyle L} ), записав коэффициент упругости как k = E ⋅ S / L . {\displaystyle k=E\cdot S/L.} Величина E {\displaystyle E} называется модулем Юнга и, в отличие от коэффициента упругости, зависит только от свойств материала стержня.

Жёсткость деформируемых тел при их соединении

При соединении нескольких упруго деформируемых тел (далее для краткости — пружин) общая жёсткость системы будет меняться. При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается.

Параллельное соединение

При параллельном соединении n {\displaystyle n} пружин с жёсткостями, равными k 1 , k 2 , k 3 , . . . , k n , {\displaystyle k_{1},k_{2},k_{3},…,k_{n},} жёсткость системы равна сумме жёсткостей, то есть k = k 1 + k 2 + k 3 + . . . + k n . {\displaystyle k=k_{1}+k_{2}+k_{3}+…+k_{n}.}

В параллельном соединении имеется n {\displaystyle n} пружин с жёсткостями k 1 , k 2 , . . . , k n . {\displaystyle k_{1},k_{2},…,k_{n}.} Из III закона Ньютона, F = F 1 + F 2 + . . . + F n . {\displaystyle F=F_{1}+F_{2}+…+F_{n}.} (К ним прикладывается сила F {\displaystyle F} . При этом к пружине 1 прикладывается сила F 1 , {\displaystyle F_{1},} к пружине 2 сила F 2 , {\displaystyle F_{2},} … , к пружине n {\displaystyle n} сила F n . {\displaystyle F_{n}.} )

Теперь из закона Гука ( F = − k x {\displaystyle F=-kx} , где x — удлинение) выведем: F = k x ; F 1 = k 1 x ; F 2 = k 2 x ; . . . ; F n = k n x . {\displaystyle F=kx;F_{1}=k_{1}x;F_{2}=k_{2}x;…;F_{n}=k_{n}x.} Подставим эти выражения в равенство (1): k x = k 1 x + k 2 x + . . . + k n x ; {\displaystyle kx=k_{1}x+k_{2}x+…+k_{n}x;} сократив на x , {\displaystyle x,} получим: k = k 1 + k 2 + . . . + k n , {\displaystyle k=k_{1}+k_{2}+…+k_{n},} что и требовалось доказать.

Последовательное соединение

При последовательном соединении n {\displaystyle n} пружин с жёсткостями, равными k 1 , k 2 , k 3 , . . . , k n , {\displaystyle k_{1},k_{2},k_{3},…,k_{n},} общая жёсткость определяется из уравнения: 1 / k = ( 1 / k 1 + 1 / k 2 + 1 / k 3 + . . . + 1 / k n ) . {\displaystyle 1/k=(1/k_{1}+1/k_{2}+1/k_{3}+…+1/k_{n}).}

В последовательном соединении имеется n {\displaystyle n} пружин с жёсткостями k 1 , k 2 , . . . , k n . {\displaystyle k_{1},k_{2},…,k_{n}.} Из закона Гука ( F = − k l {\displaystyle F=-kl} , где l — удлинение) следует, что F = k ⋅ l . {\displaystyle F=k\cdot l.} Сумма удлинений каждой пружины равна общему удлинению всего соединения l 1 + l 2 + . . . + l n = l . {\displaystyle l_{1}+l_{2}+…+l_{n}=l.}

На каждую пружину действует одна и та же сила F . {\displaystyle F.} Согласно закону Гука, F = l 1 ⋅ k 1 = l 2 ⋅ k 2 = . . . = l n ⋅ k n . {\displaystyle F=l_{1}\cdot k_{1}=l_{2}\cdot k_{2}=…=l_{n}\cdot k_{n}.} Из предыдущих выражений выведем: l = F / k , l 1 = F / k 1 , l 2 = F / k 2 , . . . , l n = F / k n . {\displaystyle l=F/k,\quad l_{1}=F/k_{1},\quad l_{2}=F/k_{2},\quad …,\quad l_{n}=F/k_{n}.} Подставив эти выражения в (2) и разделив на F , {\displaystyle F,} получаем 1 / k = 1 / k 1 + 1 / k 2 + . . . + 1 / k n , {\displaystyle 1/k=1/k_{1}+1/k_{2}+…+1/k_{n},} что и требовалось доказать.

Жёсткость некоторых деформируемых тел

Однородный стержень постоянного сечения, упруго деформируемый вдоль оси, имеет коэффициент жёсткости

где

ЕSL

Цилиндрическая витая пружина

Витая цилиндрическая пружина сжатия или растяжения, намотанная из цилиндрической проволоки и упруго деформируемая вдоль оси, имеет коэффициент жёсткости

где

dd_FnGGG

Источники и примечания

1. ↑ Упругая деформация (рус.). Архивировано 30 июня 2012 года.
2. ↑ Dieter Meschede, Christian Gerthsen. Physik. — Springer, 2004. — P. 181 ..
3. ↑ Bruno Assmann. Technische Mechanik: Kinematik und Kinetik. — Oldenbourg, 2004. — P. 11 ..
4. ↑ Динамика, Сила упругости (рус.). Архивировано 30 июня 2012 года.
5. ↑ Механические свойства тел (рус.). Архивировано 30 июня 2012 года.

ru.wikipedia.org

Определение и формула силы упругости

Определение

Силой упругости

называют силу, имеющую электромагнитную природу, которая возникает в результате деформации тела, как ответ на внешнее воздействие.

Упругой называют деформацию, при которой после прекращения действия внешней силы тело восстанавливает свои прежние форму и размеры, деформация исчезает. Деформация носит упругий характер только в том случае, если внешняя сила не превышает некоторого определенного значения, называемого пределом упругости. Сила упругости при упругих деформациях является потенциальной. Направление вектора силы упругости противоположно направлению вектора перемещения при деформации. Или по-другому можно сказать, что сила упругости направлена против перемещения частиц при деформации.

Показатели продольной эластичности

Для определенных конструкционных материалов, довольно часто используемых для достижения конкретных практических результатов, существуют уже выверенные показатели, сведенные в одну таблицу. В частности, от их параметров устойчивости к механическим воздействиям может зависеть срок службы строительных конструкций и прочих сооружений.

Цифровое установление модуля Юнга происходит с применением особой, специально рассчитанной диаграммы напряжения. Там указывается специфическая кривая, которая получается при множественных тестированиях каждого из отдельно взятых стройматериалов на устойчивость к механическим воздействиям.

Читать также: Ушм 150 с регулировкой оборотов

В таком случае физическое значение модуля продольной эластичности состоит в установлении математически точного отношения средних показателей напряжения к соответственным параметрам деформации на отдельно взятом отрезке диаграммы до конкретных, заранее установленных границ соразмерности.

Модуль Юнга

Давайте попробуем разобраться с коэффициентом упругости. Этот параметр зависит от трех величин:

• материала;
• длины L;
• площади S.

Таким образом, если удастся каким-то образом «отделить» из коэффициента длину L и площадь S, то получим коэффициент, полностью зависящий от материала.

Известно:

• чем больше площадь сечения тела, тем больше коэффициент k, причем зависимость линейная;
• чем больше длина тела, тем меньше коэффициент k, причем зависимость обратно пропорциональная.

Коэффициент упругости можно записать таким образом:

причем Е — новый коэффициент, который теперь точно зависит исключительно от типа материала.

Введем понятие “относительное удлинение”:

Эта величина более содержательна, чем

Поскольку мы уже «ввели в игру» S, то введем понятие нормального напряжения, которое записывается таким образом:

Нормальное напряжение представляет собой долю деформирующей силы на каждый элемент площади сечения.

Измеряется нормальное сечение в Н/м2.

Тогда, закон Гука можно записать в следующем виде:

подставим выражение для k:

перенесем S в левую часть, в знаменатель:

заменим величины:

Таким образом, мы получили формулу, которая отражает связь между нормальным напряжением и относительным удлинением.

Видеоурок по физике «Силы упругости. Закон Гука»:

Про закон Гука и упругие деформации:

Сформулируем закон Гука при растяжении и сжатии: при малых сжатиях нормальное напряжение прямо пропорционально относительному удлинению.

Коэффициент Е называется модулем Юнга и зависит исключительно от материала.

Что из себя представляет закон Гука для силы упругости

Если различные части твердого тела совершают неодинаковые перемещения, то в теле возникают деформации. Например, при растяжении резинового шнура, его части сместятся относительно друг друга, а сам шнур станет длиннее и тоньше — деформируется.

Далее речь будет идти только о деформациях растяжения (сжатия).

Если к вертикально расположенной пружине подвешивать тела различной массы и каждый раз при этом будет измеряться удлинение пружины с помощью шкалы, заметим, что удлинение пружины зависит от массы подвешенного груза.

Действительно, на тело массой m действует сила тяжести, равная по абсолютному значению mg→. Когда тело подвешено к пружине и находится в покое, эта сила тяжести уравновешена силой упругости пружины. Следовательно, и сила упругости пружины по абсолютному значению тоже равна mg→.

Так можно установить зависимость удлинения пружины от силы тяжести, действующей на подвешенное к ней тело. Если против делений шкалы поставить числа, указывающие в ньютонах значения силы упругости пружины, то пружина будет градуирована. Такая градуированная пружина — это прибор для измерения силы, называемый пружинным динамометром (силомером).

Опыт показывает, что при сравнительно небольших удлинениях между силой упругости пружины и ее удлинением существует линейная зависимость.

Эта зависимость была установлена английский физиком Р. Гуком еще в XVII столетии и называется законом Гука.

Если обозначить силу упругости через Fупр→, а удлинение пружины через x, то краткий закон Гука можно выразить формулой:

Знак «минус» показывает, что сила упругости направлена в противоположную сторону удлинению. Коэффициент пропорциональности называется жесткостью пружины. Данное свойство зависит от геометрических размеров материала пружины и от механических свойств материала, из которого она изготовлена. В единой системе единиц измерений жесткость пружины выражается в ньютонах на метр (Н/м).

Формула справедлива не только для пружины (это лишь наглядный пример), но также при растяжении тонкого стержня, балки или консоли.

Таким образом, закон Гука определяет следующая формулировка. 

Применение закона на практике

Закон Гука применяется как в технических и высокотехнологичных устройствах, так и в самой природе. Например, силы упругости встречаются в часовых механизмах, в амортизаторах на транспорте, в канатах, резинках и даже в человеческих костях. Принцип закона Гука лежит в основе динамометра – прибора, с помощью которого измеряют силу.

ОПРЕДЕЛЕНИЕ

Деформациями
называются любые изменения формы, размеров и объема тела. Деформация определяет конечный результат движения частей тела друг относительно друга.

ОПРЕДЕЛЕНИЕ

Упругими деформациями
называются деформации, полностью исчезающие после устранения внешних сил.

Пластическими деформациями
называются деформации, полностью или частично сохраняющиеся после прекращения действии внешних сил.

Способность к упругим и пластическим деформациям зависит от природы вещества, из которого состоит тело, условий, в которых оно находится; способов его изготовления. Например, если взять разные сорта железа или стали, то у них можно обнаружить совершенно разные упругие и пластичные свойства. При обычных комнатных температурах железо является очень мягким, пластичным материалом; закаленная сталь, наоборот, — твердый, упругий материал. Пластичность многих материалов представляет собой условие для их обработки, для изготовления из них нужных деталей. Поэтому она считается одним из важнейших технических свойств твердого вещества.

При деформации твердого тела происходит смещение частиц (атомов, молекул или ионов) из первоначальных положений равновесия в новые положения. При этом изменяются силовые взаимодействия между отдельными частицами тела. В результате в деформированном теле возникают внутренние силы, препятствующие его деформации.

Различают деформации растяжения (сжатия), сдвига, изгиба, кручения.

Неприятности с коэффициентом упругости

Физика, как известно, наука очень точная, более того, она настолько точна, что создала целые прикладные науки, измеряющие погрешности. Будучи эталоном непоколебимой точности, она не может себе позволить быть нескладной.

Практика показывает, что рассмотренная нами линейная зависимость, является ничем иным как законом Гука для тонкого и растяжимого стержня.
Лишь в качестве исключения можно применять его для пружин, но даже это является нежелательным.

Оказывается, что коэффициент k — переменная величина, которая зависит не только от того из какого материала тело, но и от диаметра и его линейных размеров.

По этой причине, наши умозаключения требуют уточнений и развития, ведь иначе, формулу:

нельзя назвать ничем иным как зависимостью между тремя переменными.

Как применить закон упругой деформации на практике

Этот закон (обобщенный для многих ситуаций) является базовым в динамике и статике тел, поэтому его применимость осуществляется в областях, где необходимо проводить расчет жесткости и напряжения деформации объектов.

В первую очередь, правило Гука необходимо применять в строительстве и технике. Так, рабочие должны точно знать, какой максимальный груз может поднять башенный кран или какую нагрузку выдержит фундамент будущего здания.

Ни один из поездов не обходится без деформации растяжения и сжатия, поэтому закон Гука справедлив и для этих ситуаций. Кроме того, механизм и принцип действия любых динамометров, которыми снабжены некоторые части технического оборудования, также основываются на этом замечательном законе.

Закон Гука выполняется во всех объектах, являющихся аналогами модели «пружинный маятник».

В обычной жизни, дома, можно видеть применимость этого закона в пружинах некоторых механизмов.

Таким образом, закон Гука применим во многих сферах жизни человека. Он является одним из базовых явлений, на которых держится существование всей жизни на планете.

Закон Гука и упругая энергия:

Закон Крюка: F = -Kx — (Eq1)

Приложенная сила прямо пропорциональна растяжению и деформации эластичного материала. Таким образом,

Напряжение прямо пропорционально деформации, поскольку напряжение — это приложенная сила к силе единицы площади, а деформация — это деформация к исходному размеру. Рассматриваемые напряжения и деформации — это нормальное напряжение и нормальная деформация.

При напряжении сдвига Материал должен быть однородным и изотропным в определенных пределах пропорциональности.

Напряжение сдвига, представленное как,

τ_xy = Gγ_xy — (Уравнение 2)

Где,

• τ_xy= напряжение сдвига
• G=модуль жесткости
• γ_xy= деформация сдвига

Это соотношение представляет собой закон Гука для напряжения сдвига. Это считается небольшим усилием и деформацией. Материал приводит к выходу из строя, если приложить нагрузку с большей силой.

Рассмотрение материала, подверженного касательным напряжениям τ_yz и τ_zy, при небольшом напряжении γ_xy будут одинаковыми для обоих условий и представлены аналогичным образом. Напряжения сдвига в пределах пропорциональности,

τ_xy = Gγ_xy — (Уравнение 3)

τ_xy = Gγ_xy — (Уравнение 4)

Случай 1: обычная деформация, когда деформации в z-направления считаются незначительными,

отношение жесткости к напряжению и деформации для изотропного и однородного материала, представленное как,

матрица жесткости сводится к простой матрице 3 × 3. матрица соответствия для плоской деформации находится путем обращения матрицы жесткости плоской деформации и определяется как

 Случай 2: Деформация плоскости:

Напряжение-деформация матрица жесткости выражается через модуль сдвига G, а инженерная деформация сдвига

представлен как,

матрица соответствия является,

Деформация и ее виды

Рассмотрим следующий случай (рисунок 2). Подвесим тело на нити.

Рисунок 2. Тело, подвешенное на нити

В таких конструкциях нить часто называют подвесом. Когда мы подвесили тело, нить начала растягиваться — в ней возникла сила упругости.

Чем больше нить растягивается, тем больше становится сила упругости. Как и в случае с опорой, как только сила упругости станет равной силе тяжести, растяжение прекратится. 

Когда возникает сила упругости?Получается, что сила упругости возникает при деформации тел. Если исчезает деформация, то исчезает и сила упругости.

Что называют деформацией тела?

Какие виды деформаций вы знаете?Иногда после таких взаимодействий тело, испытывающее деформацию, меняет свои форму и размеры — происходит неупругая (пластическая) деформация. А иногда возвращается в исходное состояние. Тогда деформация называется упругой (рисунок 3).

Рисунок 3. Упругая и пластическая деформации

Дадим определения

Упругая деформация бывает различных видов:

1. Растяжения (рисунок 2)
2. Сжатия (рисунок 4)

Рисунок 4. Деформация сжатия пружины.

1. Сдвига (при такой деформации нагрузка прикладывается параллельно основанию тела, и одна часть тела сдвигается относительно другой (рисунок 5));

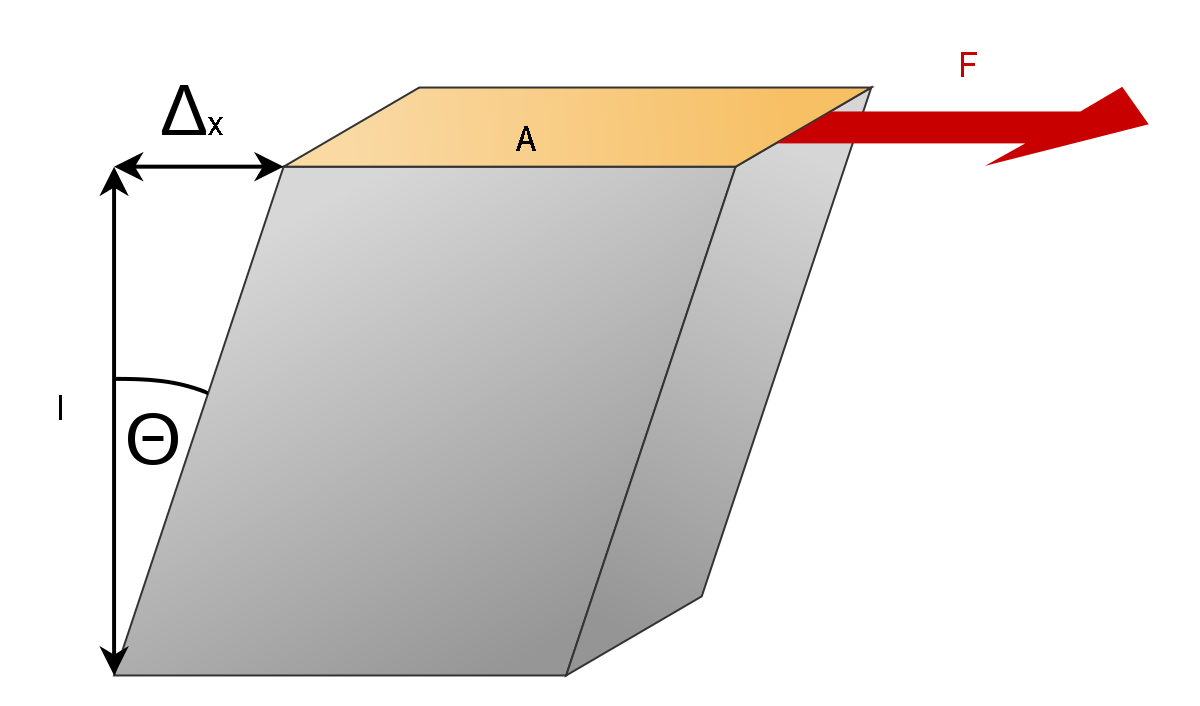Рисунок 5. Деформация сдвига.

1. Изгиба (рисунок 1);
2. Кручения (рисунок 6).

Рисунок 6. Деформация кручения

Закон Гука в математической форме

Формулировка Гука, которую мы привели выше, дает возможность записать его в следующем виде:

,

где изменение длины тела вследствие сжатия или растяжения, F сила, приложенная к телу и вызывающая деформацию (сила упругости), k коэффициент упругости, измеряется в Н/м.

Следует помнить, что закон Гука справедлив только для малых растяжений.

Также отметим, что он при растяжении и сжатии имеет один и тот же вид. Учитывая, что сила величина векторная и имеет направление, то в случае сжатия, более точной будет такая формула:

, но опять-таки, все зависит от того куда будет направлена ось, относительно которой вы проводите измерение .

В чем кардинальная разница между сжатием и растяжением? Ни в чем, если оно незначительно.

Степень применимости можно рассмотреть в таком виде:

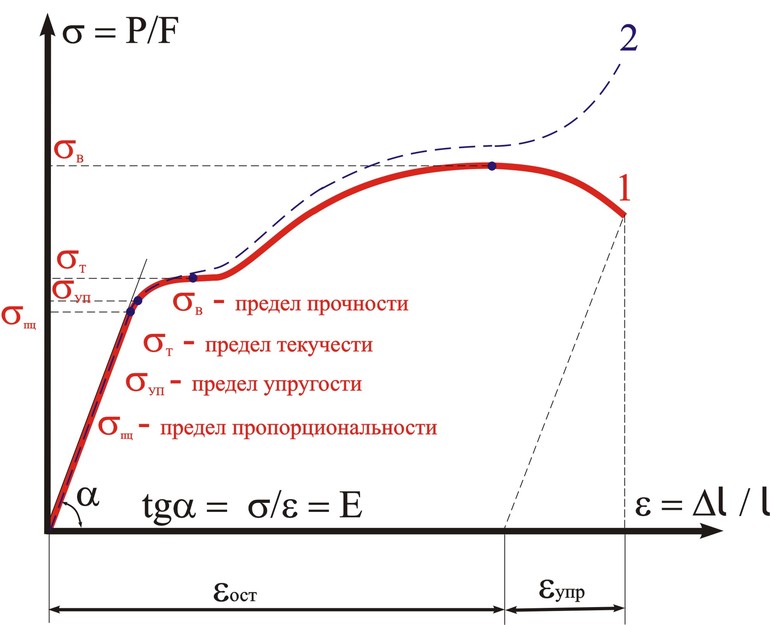
Обратим внимание на график. Как видим, при небольших растяжениях (первая четверть координат) долгое время сила с координатой имеет линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и закон перестает выполняться

На практике это отражается таким сильным растяжением, что пружина перестает возвращаться в исходное положение, теряет свойства. При еще большем растяжении происходит излом, и разрушается структура материала.

При небольших сжатиях (третья четверть координат) долгое время сила с координатой имеет тоже линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и всё вновь перестает выполняться. На практике это отражается таким сильным сжатием, что начинает выделяться тепло и пружина теряет свойства. При еще большем сжатии происходит слипание витков пружины и она начинает деформироваться по вертикали, а затем и вовсе плавиться.

Как видим формула, выражающая закон, позволяет находить силу, зная изменение длины тела, либо, зная силу упругости, измерить изменение длины:

Также, в отдельных случаях можно находить коэффициент упругости. Для того, чтобы понять как это делается, рассмотрим пример задачи:

К пружине подсоединен динамометр. Ее растянули, приложив силу в 20 Ньютон, из-за чего она стала иметь длину 1 метр. Затем ее отпустили, подождали пока прекратятся колебания, и она вернулась к своему нормальному состоянию. В нормальном состоянии ее длина составляла 87, 5 сантиметров. Давайте попробуем узнать, из какого материала сделана пружина.

Дано:

Решение:

Найдем численное значение деформации пружины:

Запишем:

Отсюда можем выразить значение коэффициента:

Посмотрев таблицу, можем обнаружить, что этот показатель соответствует пружинной стали.

Динамометры

Упругие свойства пружин используются в приборах для измерения силы. Обычно динамометр состоит из двух основных частей: пружины (упругий элемент) и шкалы устройства, на которой нанесены цифровые значения силы или массы, если этот прибор предназначен для бытового применения. Измеряемое усилие прикладывается к пружине, которая деформируется и сдвигает стрелку прибора вдоль отсчетной шкалы.

Рис. 3. Пружинные динамометры.

Хотя закон Гука и считается универсальным, но диапазон деформаций в котором он выполняется сильно отличается для разных тел. Например, в металлических проволоках (прямолинейных) и стержнях максимальная величина относительной деформации (отношение Δх к L0), для которой еще будет справедлив закон Гука, составляет не более 1%. При больших деформациях наступают необратимые разрушения материалов.

Задачи на силу упругости и закон Гука с решениями

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задача №1. Расчет силы упругости

Условие

Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.

Решение

Запишем закон Гука:

По третьему закону Ньютона:

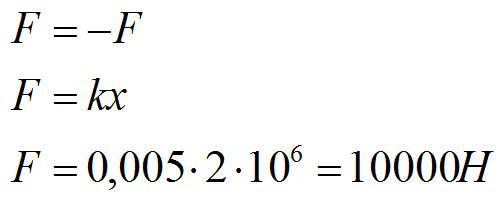
Ответ: 10 кН.

Задача №2. Нахождение жесткости пружины

Условие

Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?

Решение

По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.

Ответ: 200 Н/м

При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.

Задача №3. Нахождение ускорения тела

Условие

Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.

Решение

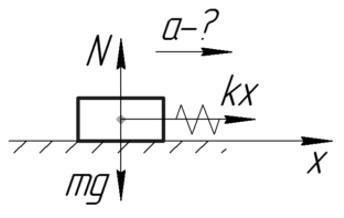
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:

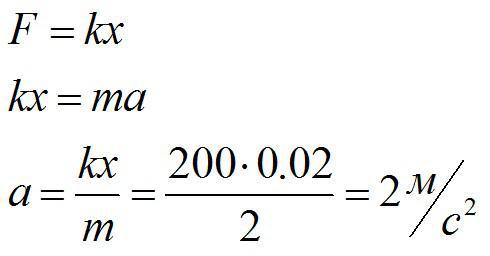
Ответ: 2 м/с^2.

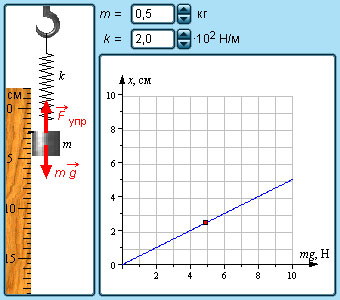
Задача №4. Нахождение жесткости пружины по графику

Условие

На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.

Решение

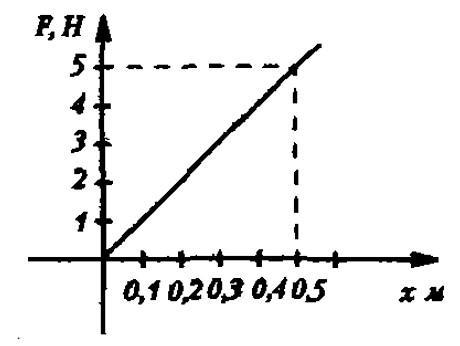
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.

Ответ: k=10 Н/м.

Задача №5. Определение энергии деформации

Условие

Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.

Решение

Энергия сжатой пружины равна:

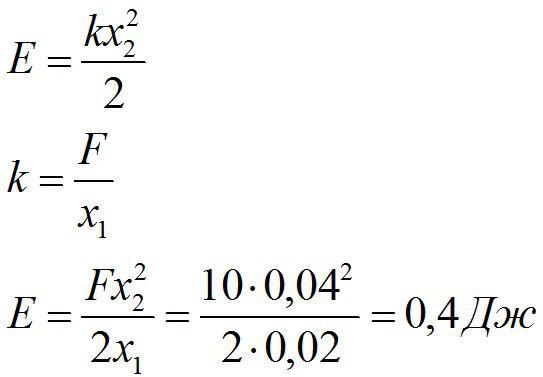
Ответ: 0,4 Дж.

Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.

При каких условиях выполняется закон Гука

А теперь посмотрим, каковы границы применимости этого выражения, и в каких условиях оно вообще выполняется.

Следует знать, что основным условием является:

s
=
E * e
,

где слева в уравнении находится напряжение, возникающее при деформации, а в правой части модуль Юнга и удлинение.

Причем, E зависит от характеристик частиц объекта, но не от его параметров формы, а второй множитель берется по модулю.

В целом аксиома Гука справедлива для многих ситуаций.

Так, при упругом изгибе пружины, лежащей на двух опорах, математическая запись теоремы выглядит следующим образом:

F
упр
= —
m * g

F
упр
= —
k * x

В иных ситуациях (при кручении, различных маятниках и других деформирующих процессах) аналогично записывается воздействие сил на объект.

Точка текучести

Тщательно проведенные эксперименты, доказывающие закон упругости, показывают, что, например, для мягкой стали и железа молекулы проволоки начинают «скользить» после того, как нагрузка превышает предел упругости, то есть материал становится пластичным. На это указывает небольшой «излом» в графике, который называется пределом текучести материала.

Переход от упругой к пластической стадии проявляется при внезапном удлинении, и когда нагрузка увеличивается, удлинение быстро растет, после чего происходит ее разрыв. Разрушающее напряжение проволоки представляет собой соответствующую силу на единицу площади поперечного сечения.

Прочность и пластичность металла, и его способность удлиняться, зависят от дефектов кристаллической решетки. Они могут состоять из отсутствующего атома в узле или дислокации в плоскости атомов. Пластическая деформация является результатом «скольжения» плоскостей. Последнее связано с движением дислокации, которая распространяется по всему кристаллу.

Таким образом, вещества, обладающие текучестью, вначале значительно удлиняются и подвергаются пластической деформации до момента разрушения. Их называют пластичными веществами, например, медь и кованое железо, являются пластичными. Если вещества, разрушаются сразу после достижения предела упругости — они называются хрупкими, например, стекло и высокоуглеродистые стали.

Суть закона

Закон назван в честь британского физика XVII века Роберта Гука, который впервые сформулировал его в 1676 году в виде анаграммы на латинском.

Он опубликовал её решение в 1678 году, утверждая, что открыл закон уже в 1660 году.

При изучении пружин и свойств их упругости, имеющих электромагнитную природу, физик отметил, что кривая зависимости напряжения от деформации для многих материалов имеет линейную область.

Вот как формулируется закон Гука: сила упругости, необходимая для растяжения упругого объекта, такого как металлическая пружина, равна или прямо пропорциональна удлинению пружины.

Эта формулировка математически записывается как F = -kx, где обозначения расшифровываются следующим образом:

1. X — это смещение конца пружины от её положения равновесия.
2. F — восстанавливающая сила, прилагаемая пружиной к этому концу.
3. K — константа пропорциональности, известная как пружинная постоянная, которая обычно измеряется в N/m (ньютон метр).

Когда действует закон Гука, поведение линейно. Если оно показано на графике или рисунке, линия, изображающая силу как функцию смещения, должна показывать прямое изменение. В правой части уравнения есть отрицательный знак, потому что восстанавливающая сила, создаваемая пружиной, находится в направлении, противоположном силе, вызвавшей смещение.

Всегда важно убедиться, что направление восстанавливающей силы задаётся последовательно при приближении к механическим задачам, связанным с упругостью. Для простых задач часто можно интерпретировать расширение X как одномерный вектор, в этом случае результирующая сила также будет одномерным вектором, а отрицательный знак в законе Гука даст правильное направление силы.. Однако успешность применения принципа зависит от того, при каких условиях он выполняется

Закон Гука является лишь линейным приближением первого порядка к реальному отклику пружин (и других упругих тел) на приложенные силы и имеет границы применимости, работая только в ограниченной системе координат.

Однако успешность применения принципа зависит от того, при каких условиях он выполняется. Закон Гука является лишь линейным приближением первого порядка к реальному отклику пружин (и других упругих тел) на приложенные силы и имеет границы применимости, работая только в ограниченной системе координат.

Поскольку ни один материал не может быть сжат сильнее определённого минимального размера (или растянут за пределы максимального размера) без некоторой постоянной деформации или изменения состояния, он применяется только до тех пор, пока задействовано ограниченное количество силы или деформации. Фактически многие материалы заметно отклонятся от закона Гука задолго до того, как будут достигнуты эти пределы упругости.

С другой стороны, этот закон является точным приближением для большинства твёрдых тел, пока силы деформации достаточно слабы.

По этой причине он широко используется во всех областях науки (например, в сопромате) и техники, а ещё является основой многих дисциплин, таких как сейсмология, молекулярная механика и акустика.

Это также принцип, стоящий за пружинной шкалой, манометром и колесом баланса механических часов.

В этом обобщённом виде закон позволяет вывести связь между деформацией и напряжением для сложных объектов, с точки зрения внутренних свойств материалов, из которых они изготовлены. Например, можно сделать вывод, что однородный стержень с равномерным поперечным сечением будет вести себя как простая пружина при растяжении, с жёсткостью K, прямо пропорциональной его площади поперечного сечения и обратно пропорциональной его длине.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Закон Гука —сила упругости k — коэффициент жесткости [Н/м] х — изменение длины (деформация)

Важно раз

Изменение длины может обозначаться по-разному в различных источниках.

Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Важно два

Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.

СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Вспомним закон Гука:

И выразим из него модуль удлинения лески:

Так как одна сила уравновешивает другую, мы можем их приравнять:

Подставим числа, жесткость лески при этом выражаем в ньютонах:

= 0,01 м = 1 см

Ответ: удлинение лески равно 1 см.