Пружинный маятник

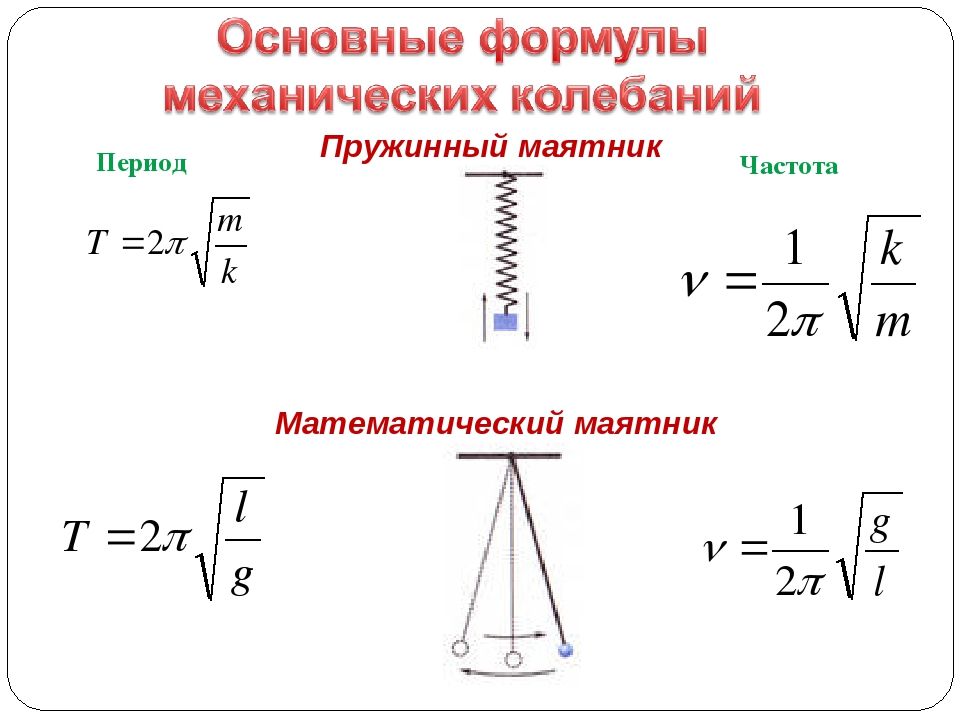
Колебание — пружинный маятник

Колебания пружинного маятника называют малыми, если сила, возникающая при смещении грузика от положения равновесия, пропорциональна его смещению и направлена в сторону положения равновесия. Для пружинного маятника условия малости колебаний удовлетворяются при смещениях, создающих возвращающую силу у пружины в пределах применимости закона Гука.
 

Колебания пружинного маятника в реальных условиях постепенно затухают, и в конце концов маятник останавливается, так как при каждом колебании часть механической энергии переходит во внутреннюю. Летящая пуля в результате трения о воздух теряет скорость, так как и у нее механическая энергия переходит во внутреннюю энергию как самой пули, так и воздуха. И никогда не бывает, чтобы рассеянная теплота снова превратилась в энергию механического движения пули.
 

Колебания пружинного маятника затухают из-за трения. Но если систематически компенсировать потери энергии, то колебания перестанут затухать. В качестве примера рассмотрим механизм возникновения незатухающих колебаний в установке, изображенной на рис. 52.1. Прикрепленная к грузу гибкая пластинка периодически прикасается к контакту, замыкая тем самым цепь электромагнита на некоторое время. В течение этого времени электромагнит притягивает груз, увеличивая его кинетическую энергию.
 

Период колебаний пружинного маятника зависит только от его массы т и коэффициента упругости k пружины, но не зависит от амплитуды колебаний.
 

Автоколебания груза на пружине.| Автоколебания камертона.

Таким образом колебание пружинного маятника, которое само по себе затухало бы, поддерживается периодическими толчками, обусловленными самим колебан и е м маятника. При каждом толчке батарея отдает порцию энергии, часть которой идет на подъем груза.
 

Для возникновения колебаний пружинного маятника ему необходимо сообщить механическую энергию. Первоначально это была потенциальная энергия растянутой пружины. При движении груза к положению равновесия его потенциальная энергия уменьшается, кинетическая же увеличивается и становится максимальной в положении равновесия. В дальнейшем продолжается переход одного вида энергии в другой.
 

Свободные затухающие колебании пружинного маятника.
 

Автоколебания камертона.

Таким образом, колебание пружинного маятника, которое само по себе затухало бы, поддерживается периодическими толчками, обусловленными самим колебание м маятник а. При каждом толчке батарея отдает порцию энергии, часть которой идет на подъем груза. Система сама управляет действующей на нее силой, сама регулирует поступление энергии из источника — батгрои В. Колебания не затухают именно потому, что за каждый период от батареи отбирается как раз такое количестве энергии, кпкое расходуется за то же время на трение и другие потери.
 

Автоколебания груза на пружине.

Таким образом, колебание пружинного маятника, которое само по себе затухало бы, поддерживается периодическими толчками, обусловленными самим колебанием маятника. При каждом толчке батарея отдает порцию энергии, часть которой идет на подъем груза. Система сама управляет действующей на нее силой и регулирует поступление энергии из источника — батареи. Колебания не затухают именно потому, что за каждый период от батареи отбирается как раз столько энергии, сколько расходуется за то же время на трение и другие потери.
 

Автоколебания камертона.

Таким образом, колебание пружинного маятника, которое само по себе затухало бы, поддерживается периодическими толчками, обусловленными самим колебанием маятника. При каждом толчке батарея отдает порцию энергии, часть которой идет на подъем груза. Система сама управляет действующей на нее силой, сама регулирует поступление энергии из источника — батареи В. Колебания не затухают именно потому, что за каждый период от батареи отбирается как раз такое количество энергии, какое расходуется за то же время на трение и другие потери.
 

Автоколебания груза на пружине.

Постигаем закон Гука

Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.

Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину ​\( x \)​, потребуется приложить внешнюю силу ​\( F_{вн} \)​, которая равна:

где ​\( k \)​ — это коэффициент пропорциональности.

Точнее говоря, вектор деформации ​\( \mathbf{x} \)​ всегда направлен противоположно силе сопротивления пружины (или силе упругости) \( \mathbf{F} \), а потому в векторную формулировку закона Гука обычно входит знак “минус”:

Растягиваем и сжимаем пружины

В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности ​\( k \)​ в законе Гука ​\( F=kx \)​ называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.

Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?

Вес автомобиля равен ​\( mg \)​, где ​\( g \)​ — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка ​\( mg/4 \)​.

Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:

т.е. коэффициент упругости равен:

Подставляя значения, получим:

Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·103 Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.

Изучаем особенности закона Гука

Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:

Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.

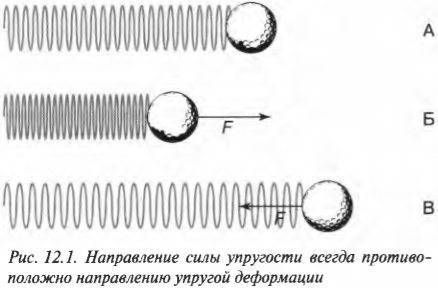
Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

Формула для пружинного маятника. Задача №2

Формулы маятников имеют общую часть, а именно 2п. Эта величина присутствует сразу в двух формулах, но разнятся они подкоренным выражением. Если в задаче, касающейся периода пружинного маятника, указана масса груза, то избежать вычислений с ее применение невозможно, как это было в случае с математическим маятником. Но пугаться не стоит. Вот так выглядит формула периода для пружинного маятника:

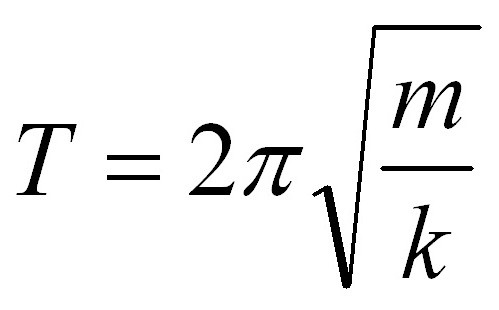
В ней m — масса подвешенного к пружине груза, k — коэффициент жесткости пружины. В задаче значение коэффициента может быть приведено. Но если в формуле математического маятника особо не разгуляешься — все-таки 2 величины из 4 являются константами — то тут добавляется 3 параметр, который может изменяться. И на выходе мы имеем 3 переменных: период (частота) колебаний, коэффициент жесткости пружины, масса подвешенного груза. Задача может быть сориентирована на нахождение любого из этих параметров. Вновь искать период было бы слишком легко, поэтому мы немного изменим условие. Найдите коэффициент жесткости пружины, если время полного колебания составляет 4 секунды, а масса груза пружинного маятника равна 200 граммам.

Для решения любой физической задачи хорошо бы сначала сделать рисунок и написать формулы. Они здесь — половина дела. Записав формулу, необходимо выразить коэффициент жесткости. Он у нас находится под корнем, поэтому обе части уравнения возведем в квадрат. Чтобы избавиться от дроби, умножим части на k. Теперь оставим в левой части уравнения только коэффициент, то есть разделим части на T^2. В принципе, задачку можно было бы еще немного усложнить, задав не период в числах, а частоту. В любом случае, при подсчетах и округлениях (мы условились округлять до 3-его знака после запятой), получится, что k = 0, 157 Н/м.

Учебное особие по физике

Пружинный маятник

Пружинный маятник — это колебательная система, состоящая из материальной точки массой т и пружины. Рассмотрим горизонтальный пружинный маятник (рис. 1, а). Он представляет собой массивное тело, просверленное посередине и надетое на горизонтальный стержень, вдоль которого оно может скользить без трения (идеальная колебательная система). Стержень закреплен между двумя вертикальными опорами.

К телу одним концом прикреплена невесомая пружина. Другой ее конец закреплен на опоре, которая в простейшем случае находится в покое относительно инерциальной системы отсчета, в которой происходят колебания маятника. В начале пружина не деформирована, и тело находится в положении равновесия С. Если, растянув или сжав пружину, вывести тело из положения равновесия, то со стороны деформированной пружины на него начнет действовать сила упругости, всегда направленная к положению равновесия.

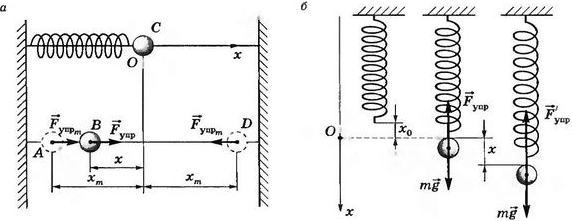
Рис. 1

Пусть мы сжали пружину, переместив тело в положение А, и отпустили . Под действием силы упругости оно станет двигаться ускоренно. При этом в положении А на тело действует максимальная сила упругости, так как здесь абсолютное удлинение x_m пружины наибольшее. Следовательно, в этом положении ускорение максимальное. При движении тела к положению равновесия абсолютное удлинение пружины уменьшается, а следовательно, уменьшается ускорение, сообщаемое силой упругости. Но так как ускорение при данном движении сонаправлено со скоростью, то скорость маятника увеличивается и в положении равновесия она будет максимальна.

Достигнув положения равновесия С, тело не остановится (хотя в этом положении пружина не деформирована, и сила упругости равна нулю), а обладая скоростью, будет по инерции двигаться дальше, растягивая пружину. Возникающая при этом сила упругости направлена теперь против движения тела и тормозит его. В точке D скорость тела окажется равной нулю, а ускорение максимально, тело на мгновение остановится, после чего под действием силы упругости начнет двигаться в обратную сторону, к положению равновесия. Вновь пройдя его по инерции, тело, сжимая пружину и замедляя движение, дойдет до точки А (так как трение отсутствует), т.е. совершит полное колебание. После этого движение тела будет повторяться в описанной последовательности. Итак, причинами свободных колебаний пружинного маятника являются действие силы упругости, возникающей при деформации пружины, и инертность тела.

По закону Гука F_x = -kx. По второму закону Ньютона F_x = ma_x. Следовательно, ma_x = -kx. Отсюда

— динамическое уравнение движения пружинного маятника.

Видим, что ускорение прямопропорционально смешению и противоположно ему направлено. Сравнивая полученное уравнение с уравнением гармонических колебаний , видим, что пружинный маятник совершает гармонические колебания с циклической частотой

— период колебаний пружинного маятника.

По этой же формуле можно рассчитывать и период колебаний вертикального пружинного маятника (рис. 1. б). Действительно, в положении равновесия благодаря действию силы тяжести пружина уже растянута на некоторую величину x, определяемую соотношением mg = kx. При смещении маятника из положения равновесия O на х проекция силы упругости

и по второму закону Ньютона

Подставляя сюда значение kx = mg, получим уравнение движения маятника

совпадающее с уравнением движения горизонтального маятника.

Слайды и текст этой презентации

Слайд 1

Текст слайда:

Исследование зависимости периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды колебаний и температуры воздуха.

Работа учащихся 9 класса МОУ «Старовыслинская ООШ»Шингалова Радия и Надукова Дениса

2011г. Учитель: Потапов Н.А.

Слайд 2

Текст слайда:

Цель нашей работы:

Исследовать зависимость периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды колебаний и температуры воздуха.

Слайд 3

Текст слайда:

Введение.

В настоящее время в технике и быту используются различные виды пружины. Твердые тела и материалы, которыми располагает человечество, во многом определяет уровень его технического развития. Изучая свойства твердых тел, мы заинтересовались упругими свойствами пружины и решили исследовать их.

Слайд 4

Текст слайда:

Подготовка к эксперименту

Для проведения экспериментов подобрали следующее оборудование: штатив с 2-мя лапками, пружина №1 (к1=6,4 Н/м), пружина №2 (к2=21,6Н/м), набор грузов массой по 100г, линейка, секундомер, динамометр.

Слайд 5

Текст слайда:

ПЕРИОД КОЛЕБАНИЯ

Одной из важных характеристик колебательного движения является период колебания – интервал времени, в течение которого происходит одно полное колебание. Связь периода колебаний пружинного маятника от массы груза и жёсткости пружины известна:

Слайд 6

Текст слайда:

План проведения эксперимента:

Приготовить приборы и оборудования.Исследовать зависимость периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды и температуры воздуха. Заполнение таблиц измерений.Вычерчивание графиков зависимостей.Анализ графиков зависимостей периода от разных параметров. Обобщение результатов.

Слайд 7

Текст слайда:

Эксперимент 1
Исследование зависимости периода колебаний пружинного маятника от массы груза.

Подвесим к штативу пружину №1. Возьмем гирю массой 100г и прикрепим к пружине. С помощью секундомера определим время 10 колебаний пружинного маятника. Повторим эксперимент с гирями 200г и 300г. Определим по формуле период колебаний:

Результаты измерений и вычислений запишем в таблицу 1:

Слайд 8

Текст слайда:

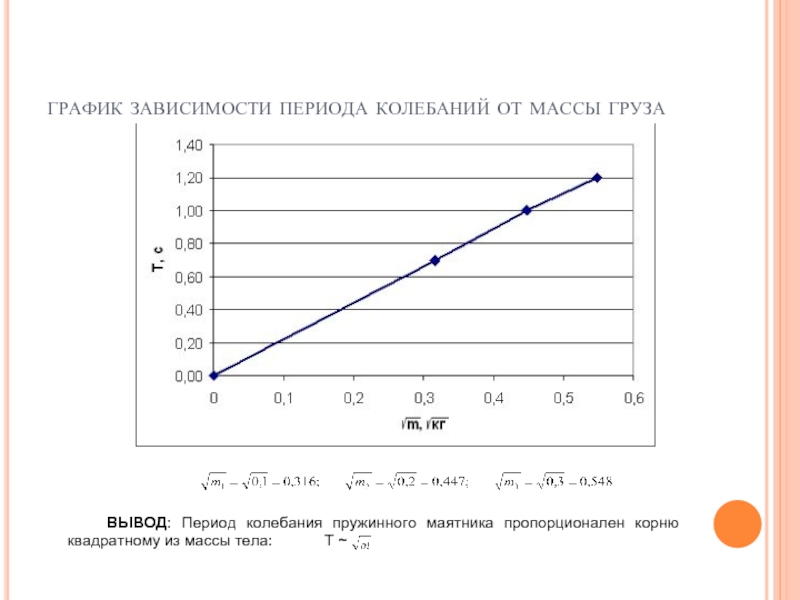
график зависимости периода колебаний от массы груза

ВЫВОД: Период колебания пружинного маятника пропорционален корню квадратному из массы тела: Т ~

.

Слайд 9

Текст слайда:

Эксперимент 2
Исследование зависимости периода колебаний пружинного маятника от жёсткости пружины

Подвесим к штативу пружину №2. Возьмем гирю массой 100г и прикрепим к пружине. С помощью секундомера определим время 10 колебаний пружинного маятника. Повторим эксперимент с гирями 200г и 300г. Определим по формуле период колебаний:

Результаты измерений и вычислений запишем в таблицу 2:

Слайд 10

Текст слайда:

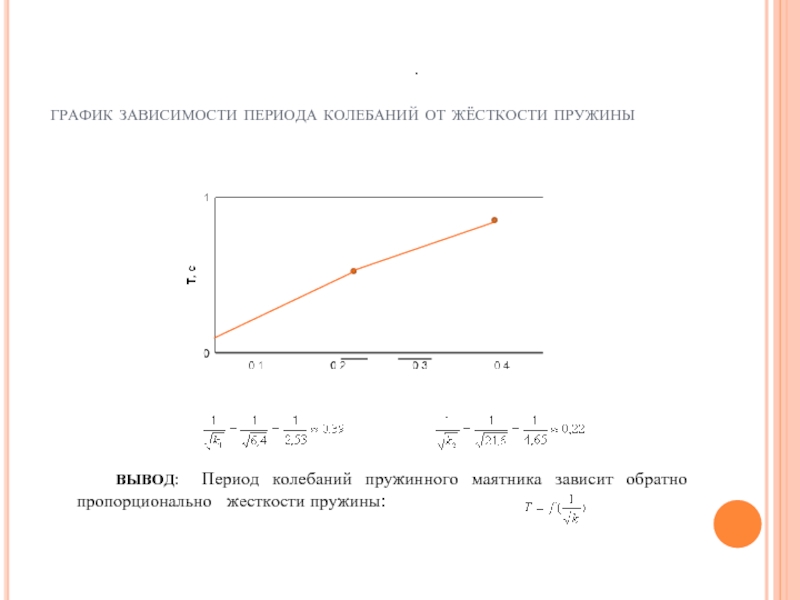
график зависимости периода колебаний от жёсткости пружины

ВЫВОД: Период колебаний пружинного маятника зависит обратно пропорционально жесткости пружины:

.

Слайд 11

Текст слайда:

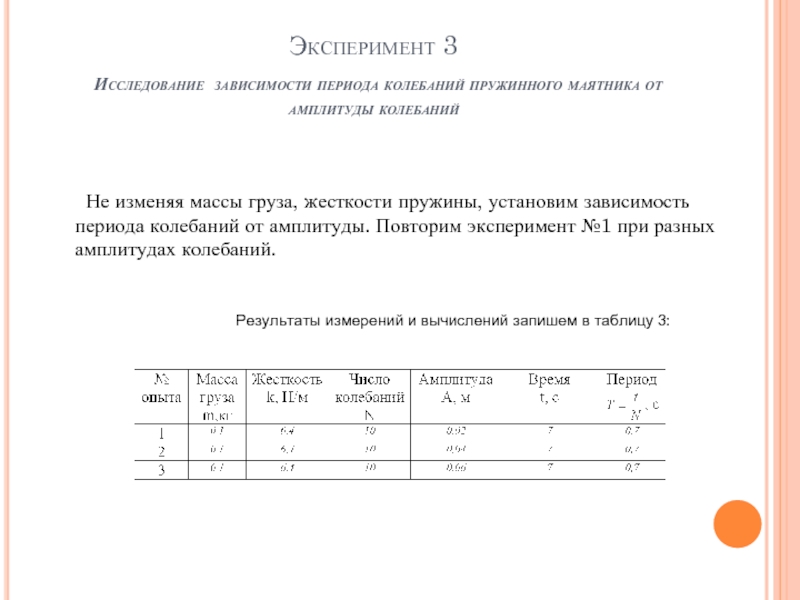
Эксперимент 3
Исследование зависимости периода колебаний пружинного маятника от амплитуды колебаний

Результаты измерений и вычислений запишем в таблицу 3:

Не изменяя массы груза, жесткости пружины, установим зависимость периода колебаний от амплитуды. Повторим эксперимент №1 при разных амплитудах колебаний.

Слайд 12

Текст слайда:

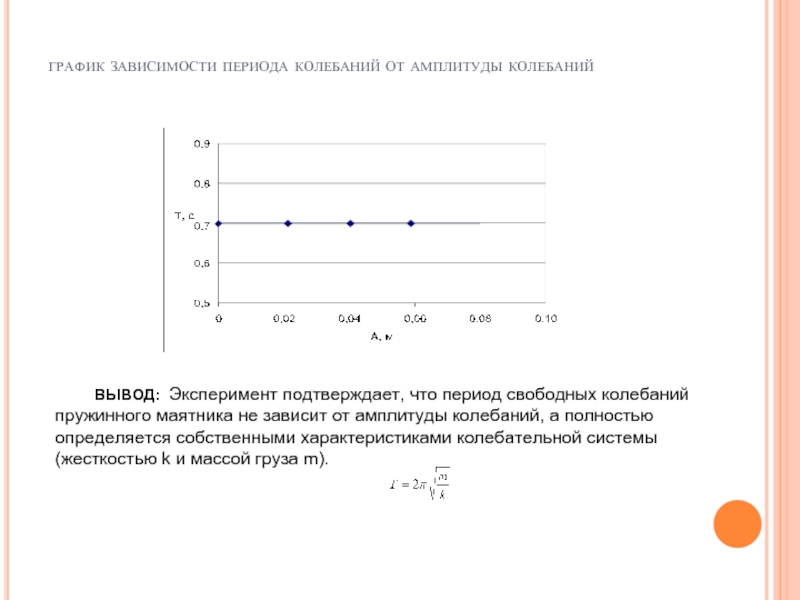
график зависимости периода колебаний от амплитуды колебаний

ВЫВОД: Эксперимент подтверждает, что период свободных колебаний пружинного маятника не зависит от амплитуды колебаний, а полностью определяется собственными характеристиками колебательной системы (жесткостью k и массой груза m).

Слайд 13

Текст слайда:

Эксперимент 4
Исследование зависимости периода колебаний пружинного маятника от температуры.

Для исследования зависимости периода колебаний пружинного маятника от температуры повторили эксперимент №1 во дворе школы при другой температуре ( t= -20 0С ).

ВЫВОД: Период колебания пружинного маятника не зависит от температуры.

Слайд 14

Текст слайда:

Обобщение

В результате экспериментов мы выяснили, что период колебаний пружинного маятника зависит от массы тела, жёсткости пружины и не зависит от амплитуды колебаний и температуры.

Слайд 15

Текст слайда:

Литература:

Учебник по физике для 9 класса средней школы Н.М. Шахмаева, С.Н. Шахмаева, Д.Ш. Шодиева,-М. Просвещение.1990г. Кикоин И.К., Кикоин А.К. Физика. Учебник для 9кл.-М. Просвещение, 1990г.Громов С.В. , Родина Н.А.. Физика. Учеб. Для 8кл.-М. Просвещение. 2000г.Сеть Интернет.

Темы по физике

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

Темы по математике

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Свободные колебания пружинного маятника

Рассматривая то, чем вызваны свободные колебания пружинного маятника следует уделить внимание действию внутренних сил. Они начинают формироваться практически сразу после того, как телу было передано движение. Особенности гармонических колебаний заключаются в нижеприведенных моментах:

Особенности гармонических колебаний заключаются в нижеприведенных моментах:

1. Могут также возникать и другие типы сил воздействующего характера, который удовлетворяют все нормы закона, называются квазиупругими.
2. Основными причинами действия закона могут быть внутренние силы, которые формируются непосредственно на момент изменения положения тела в пространстве. При этом груз обладает определенной массой, усилие создается за счет фиксации одного конца за неподвижный объект с достаточной прочностью, второго за сам груз. При условии отсутствия трения тело может совершать колебательные движения. В этом случае закрепленный груз называется линейным.

Не стоит забывать о том, что существует просто огромное количество различных видов систем, в которых осуществляется движение колебательного характера. В них также возникает упругая деформация, которая становится причиной применения для выполнения какой-либо работы.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Разделы: Физика

Класс: 9

На уроке хотелось бы сразу дать учащимся в сравнении колебания пружинного и математического маятников

Обратить внимание на сходство процессов, одинаковое изменение энергий (кинетической и потенциальной) через одинаковые промежутки времени

Пояснение по форме объяснения учебного материала: на доске удобнее расположить рисунки маятников рядом, разделив доску пополам. Записи для описания характеристик маятников делать на одном уровне.

Цели урока:

1. Ввести понятия колебательных систем,
2. Рассмотреть на примерах математического и пружинного маятников особенность свободных колебаний.
3. Определение параметров идеальных колебательных систем.
4. Научить выделять существенные признаки колебательных систем.
5. Формирование потребности в новых знаниях, усвоение предмета.

Демонстрации:

1. Математический маятник.
2. Пружинный маятник.

смещение положения равновесия точки

смещение положения равновесия точки

Задача 40713

Написать уравнение синусоидального гармонического колебания, если амплитуда скорости 63 см/с, период колебаний 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найти амплитуду ускорения, частоту колебаний.

Задача 40738

Написать уравнение гармонического колебания, совершаемого по закону косинуса, если амплитуда ускорения 50 см/с2, частота колебаний 50 Гц, смещение точки от положения равновесия в начальный момент времени 25 мм. Найти амплитуду скорости.

Задача 40739

Написать уравнение гармонического колебания, совершаемого по закону косинуса, если амплитуда ускорения 50 м/с2, частота колебаний 50 Гц, смещение точки от положения равновесия в начальный момент времени 0,25 мм. Найти амплитуду скорости.

Задача 26216

Написать уравнение гармонических колебаний с амплитудой 50мм, периодом 4с и начальной фазой П/4. Найти смещение точки от положения равновесия при t = 0 и t = 1,5 с.

Задача 26560

Уравнение незатухающих колебаний дано в виде: У = 4 ·10–2cos6πt, м. Найти смещение от положения равновесия точки, находящейся на расстоянии 75 см от источника колебаний через 0,01 с после начала колебаний. Скорость распространения колебаний 340 м/с.

Задача 11103

Напишите уравнение гармонического колебания, если амплитуда скорости vm = 63 см/с, период колебаний Т = 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найдите амплитуду ускорения и частоту колебаний. Постройте график зависимости смещения от времени.

Задача 12666

На каком ближайшем расстоянии от источника колебаний с периодом 45 мс через время, равное половине периода после включения источника смещение точки от положения равновесия равно половине амплитуды? Скорость распространения колебаний равна 158 м/с. Считать, что в момент включения источника все точки находятся в положении равновесия.

Задача 14576

Уравнение незатухающих колебаний х = 4sin(600πt) см. Найти смещение x от положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01с после начала колебаний. Скорость распространения колебаний v = 300 м/с.

Задача 14932

Плоская монохроматическая волна распространяется вдоль оси Y. Амплитуда волны А = 0,05 м. Считая, что в начальный момент времени смещение точки Р, находящейся в источнике, максимально, определить смещение от положения равновесия точки М, находящейся на расстоянии у = λ/2 от источника колебаний в момент времени t = T/6.

Задача 15330

Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника колебаний, в момент времени Т/6 равно половине амплитуды. Найти длину бегущей волны.

Задача 17372

Начальная фаза гармонического колебания ψ = 0. При смещении точки от положения равновесия х1 = 2,4 см скорость точки v1 = 3 см/с, а при смещении х2 = 2,8 см ее скорость v2 = 2 см/с. Найти амплитуду А и период Т этого колебания.

Задача 19324

На каком расстоянии от источника колебаний, совершаемых по закону синуса, в момент времени t = T/2 смещение точки от положения равновесия равно половине амплитуды? Скорость распространения колебаний 340 м/с. Период колебаний 10–3 с.

Задача 19326

Источник плоских волн совершает колебания по закону x = A cos ωt. Через четверть периода после начала колебаний смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника, равно половине амплитуды. Найти длину бегущей волны.

Задача 19327

Источник плоских волн совершает колебания по закону x = A cos ωt. Какова амплитуда колебаний, если смещение от положения равновесия точки, отстоящей от источника на расстоянии λ/12 для момента времени T/4, равно 0,025 м?

Задача 20380

Определить начальную фазу колебаний, которые происходят по закону косинуса, если максимальная скорость равна 16 см/с, период колебаний 1,4 с, а смещение точки от положения равновесия в начальный момент времени составляет 2,84 см.