Как найти стороны прямоугольного треугольника

Гипотенуза

Перейдем непосредственно к гипотенузе треугольника. Гипотенуза – это наибольшая сторона треугольника. Гипотенуза всегда больше любого из катетов, но при этом всегда меньше суммы катетов. Это следствие из теоремы неравенства треугольника.

Теорема гласит: в треугольнике ни одна из сторон не может больше суммы двух других. Существует и вторая формулировка или вторая часть теоремы: в треугольнике напротив большей стороны лежит больший угол и наоборот.

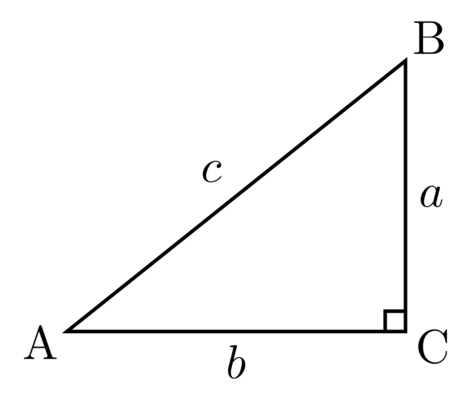Рис. 2. Прямоугольный треугольник.

В прямоугольном треугольнике большим углом является прямой угол, так как второго прямого угла или тупого угла быть не может по уже названным причинам. Значит напротив прямого угла всегда лежит большая сторона.

Кажется непонятным, почему именно прямоугольный треугольник заслужил отдельное наименование каждой из сторон. На самом деле, в равнобедренном треугольнике стороны так же носят свои названия: боковые стороны и основание. Но именно за катеты и гипотенузы учителя особенно любят ставить двойки. Почему? С одной стороны это дань памяти древним грекам, изобретателям математики. Именно они изучали прямоугольные треугольники и наряду с этими знаниями оставили целый пласт информации, на котором строится современная наука. С другой же стороны существование этих названий значительно упрощает формулировки теорем и тригонометрических тождеств.

Формула гипотенузы равнобедренного прямоугольного треугольника

1001student.ru > Геометрия > Формула гипотенузы равнобедренного прямоугольного треугольника

В повседневной жизни каждому человеку время от времени приходится решать задачи из школьной программы.

Несмотря на то что многие в детстве считали эти знания ненужными, сейчас все понимают, что были неправы.

Например, в любой момент может понадобиться найти длину гипотенузы равнобедренного треугольника, формулу расчета которой несложно вывести самостоятельно. Для этого следует вспомнить законы геометрии.

Законы геометрии

В первую очередь надо определиться с терминами. Чтобы в дальнейшем было понятно, что означают те или иные геометрические понятия, необходимо вспомнить следующие определения:

треугольник;
сторона;
угол;
бедро;
равнобедренный;
равносторонний;
прямоугольный;
гипотенуза;
катет;
теорема.

Треугольник – это замкнутая геометрическая фигура, состоящая из трех точек, соединенных последовательно тремя отрезками, которые являются сторонами этой фигуры. Прямые, исходящие из одной точки, образуют угол.

Каждый треугольник состоит из трех сторон. Исходящие из одной вершины стороны называются бедрами, поэтому фигура, у которой минимум две стороны имеют равную длину, называется равнобедренной. В случае когда все стороны фигуры равны, она называется равносторонним треугольником.

Треугольник, в котором есть прямой угол, называется прямоугольным. Прямым в геометрии называется угол в 90 градусов. Поскольку в каждой треугольной фигуре сумма всех углов равна 180 градусов, то в ней может быть только один прямой угол. Гипотенуза в переводе с греческого языка означает «натянутая» – это сторона треугольника, которая лежит напротив прямого угла.

Катет – это одна из двух других сторон прямоугольного треугольника, тоже греческое слово, которое в переводе означает опущенный, отвесный или перпендикуляр. Катеты одновременно являются бедрами, а в равнобедренном прямоугольном треугольнике гипотенуза служит еще и основанием.

Теорема – это истина, которую надо доказать. Одно из самых известных и значимых правил геометрии – это теорема Пифагора.

Теорема Пифагора

Древнегреческий математик и философ Пифагор, если верить историкам, первым нашел правильный расчет соотношения размеров длин катетов и гипотенузы. Согласно теореме Пифагора, длина гипотенузы в квадрате равна сумме длин катетов, возведенных в квадрат. Можно кратко описать теорему, обозначив гипотенузу буквой Г, а катеты — К1 и К2:

Г2 =К12 + К22

Как вычислить формулу

Если довериться логике и Пифагору, то легко высчитать, что размер самой длинной стороны треугольника будет равен квадратному корню из суммы квадратов двух меньших сторон. Если учесть, что в равнобедренном треугольнике катеты равны, то формулу можно усовершенствовать.

Гипотенузу равнобедренного треугольника можно рассчитать путем вычисления квадратного корня из квадрата длины катета, умноженного на два.

Вопрос на засыпку

Чтобы ответить на вопрос, как найти гипотенузу равностороннего треугольника, надо вспомнить, чему равен каждый его угол.

При любой длине сторон в этой фигуре, сумма всех углов неизменна и равна 180 градусов, соответственно каждый из них в этой фигуре равен 60 градусов.

Прямого угла в такой фигуре не может быть по определению, поэтому нет и гипотенузы. Значит, поставленный вопрос некорректен и не имеет ответа.

Практическое применение

В каких сферах повседневной жизни может понадобиться знание формулы? Эта тема находит практическое применение в архитектуре, строительстве, физике, математике, астрономии и других областях народного хозяйства, например:

Для дизайнера, работающего над планировкой дома или квартиры, важно знать, является ли конкретный угол прямым. Высчитав длину всех сторон, можно сделать вывод о размере угла.
В организациях, занимающихся оптовой торговлей или транспортными услугами, для правильного построения логистической схемы распределения товара между розничными точками порой необходимо рассчитывать самые краткие и оптимальные пути передвижения между различными объектами.
На даче или огороде можно правильно рассчитать длину лестницы, необходимой для установки на определенную высоту под определенным углом, чтобы легко взбираться на мансарду или чердак.. Если внимательно оглядеться вокруг, можно различить большое количество разнообразных геометрических фигур

Если внимательно оглядеться вокруг, можно различить большое количество разнообразных геометрических фигур.

Где геометрия, там и возможности использовать ее правила и формулы расчетов, в том числе и формулу длины гипотенузы.

Треугольник

Треугольник – это фигура, состоящая из трех отрезков (сторон) и трех точек (вершин). Стороны образуют три угла при трех вершинах.

Рис. 1. Треугольник

Для формулировки теорем требуется всем понятное обозначение сторон. Эти обозначения не обязательно должны быть классическими АВ или ВС, обозначения зависят от каждого конкретного ученика. Никто не вправе запретить решающему обозначать фигуру так, как это удобно лично ему. Например, именно по этой причине в математику было введено понятие основания треугольника. Вспомните, в равнобедренном треугольнике высота, проведенная к основанию, совпадает с биссектрисой и медианой. Формулировка четкая, понятная и простая для запоминания. Именно в этих целях и вводят дополнительные понятия.

Применение теоремы

Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.

Расстояние между точками

Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:

\(\ s=\sqrt{(a-с)^{2} + (b-d)^{2}}\), где:

s – необходимое расстояние;
(a; b) и (с; d) – координаты двух точек.

Евклидова метрика

В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:

\(d(p,\;q)=\sqrt{\sum_{i=1}^n{(p_i-q_i)}^2}\), где:

n – число измерений данного пространства;
d (p, q) – необходимое расстояние;
p(p₁,….,pn) и q(q₁,….,q_n) – две точки, расстояние между которыми нужно найти.

Теория чисел

Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.

Определение

Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.

Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.

Терминология и особые случаи

Прямоугольный треугольник и его элементы.

Гипотенуза – это длинная сторона прямоугольного треугольника и сторона, лежащая против прямого угла . Две меньшие стороны называются катетами , те, которые составляют прямой угол; каждая нога противопоставлена под острым углом. Только если мерой трех сторон являются целые числа , они составляют трио с пифагорейским тройным именем .

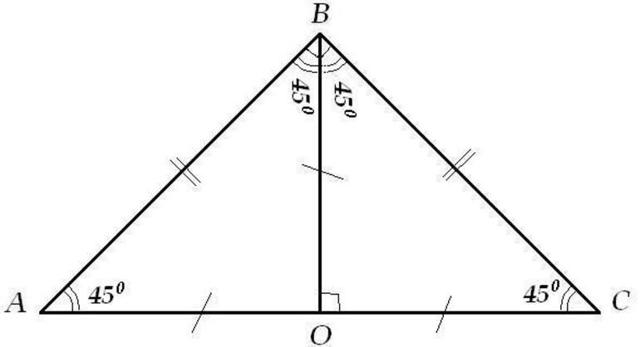
Если катеты равны, то треугольник называется равнобедренным прямоугольным (45-90-45); существование

это⁡число Пи4знак равноногагипотенузазнак равно22{\displaystyle \operatorname {sen} {\frac {\pi }{4}}={\frac {\text{cateto}}{\text{hipotenusa}}}={\frac {\sqrt {2}}{2}}}

Хорошо известен разносторонний прямоугольный треугольник, у которого меньший катет равен половине гипотенузы, и эти две стороны образуют острый угол 30º, а другой угол 60º, (30-90-60) и получается путем деления пополам равносторонний треугольник по высоте; эти причины возникают между указанными сторонами. Если допустить, что сторона равностороннего треугольника равна , и с помощью высоты получится два прямоугольных треугольника, в каждом из которых гипотенуза равна ; катет, противоположный углу 30º, и катет, противоположный углу 60º, получают следующие значения для соответствующих синусов:
2a{\displaystyle 2a}2a{\displaystyle 2a}a{\displaystyle a}a3{\displaystyle a{\sqrt {3}}}

1. sen⁡π6=cateto menorhipotenusa=a2a=12{\displaystyle \operatorname {sen} {\frac {\pi }{6}}={\frac {\text{cateto menor}}{\text{hipotenusa}}}={\frac {a}{2a}}={\frac {1}{2}}}

2. sen⁡π3=cateto mayorhipotenusa=a32a=32{\displaystyle \operatorname {sen} {\frac {\pi }{3}}={\frac {\text{cateto mayor}}{\text{hipotenusa}}}={\frac {a{\sqrt {3}}}{2a}}={\frac {\sqrt {3}}{2}}}

Всегда ли треугольник 3 4 5 прямоугольный?

Любой треугольник, стороны которого находятся в соотношении 3: 4: 5, является прямоугольный треугольник. Такие треугольники, стороны которых относятся к целым числам, называются пифагорейскими тройками. … Если вы умножите стороны на любое число, результатом все равно будет прямоугольный треугольник, стороны которого относятся как 3:4:5.

Также Как найти недостающую длину неправильной формы?

Когда нельзя использовать теорему Пифагора?

Это прямоугольный треугольник; при суммировании квадратов длин сторон, вы получите квадрат длины гипотенузы. Неправильно. Это не прямоугольный треугольник, поэтому вы не можете использовать теорему Пифагора, чтобы найти r.

Для чего не используется теорема Пифагора? Нет, мы не можем использовать теорему Пифагора для всех треугольников Как гласит теорема Пифагора, «если известны длины любых двух сторон, то можно найти длину третьей стороны. Другое следствие теоремы состоит в том, что в любом прямоугольном треугольнике гипотенуза больше любой из других сторон, но меньше их суммы».

Формулировка теоремы

Изначальная (геометрическая) формулировка Пифагора гласила:

Теорема

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Позднее появился алгебраический вариант:

Теорема

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.

Доказательство Дж. Гарфилда

Джеймс Гарфилд — двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.

В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.

Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.

Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.

S=а+в/2 * (а+в)

Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:

S=ав/2 *2 + с 2 /2

Теперь необходимо уравнять два исходных выражения

2ав/2 + с/2=(а+в) 2 /2

с 2 =а 2 +в 2

О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

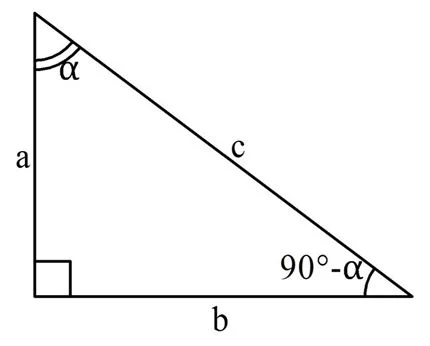
Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

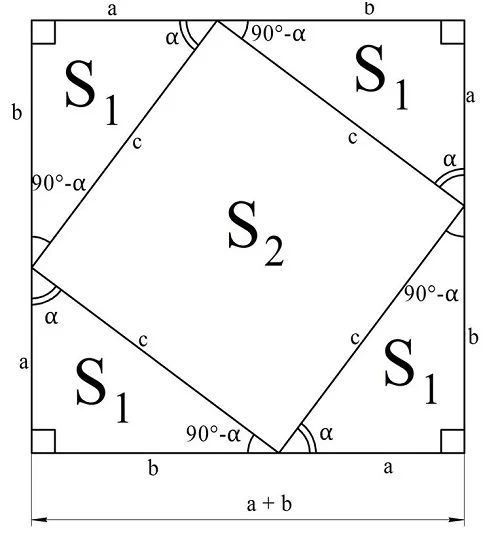
Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

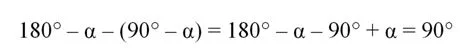
Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

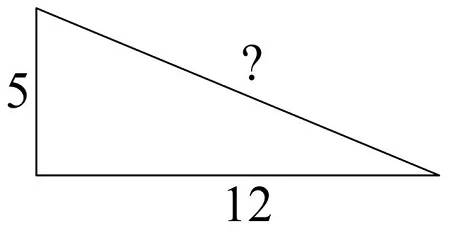
Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

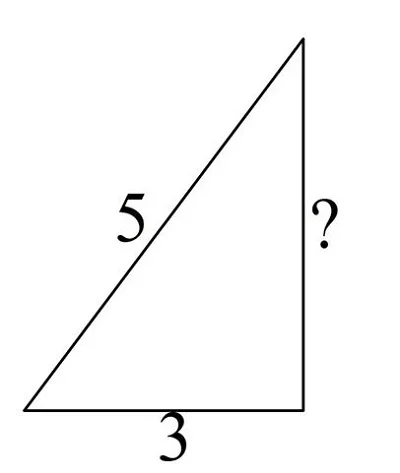
Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

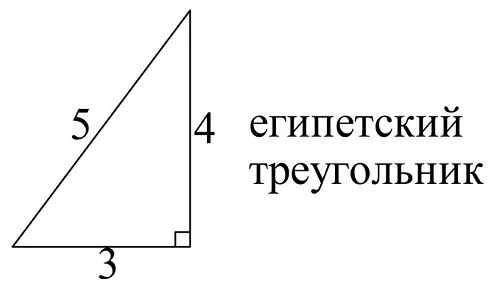
Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами

Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

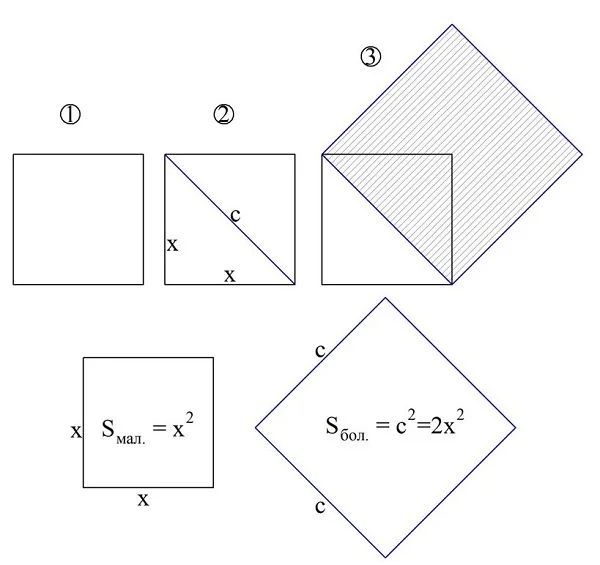
Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х2. Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с2– это площадь большого (на рисунке – синего)квадрата, а х2 – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

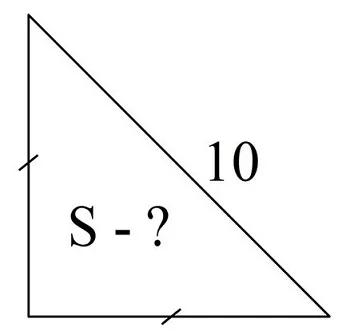
Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

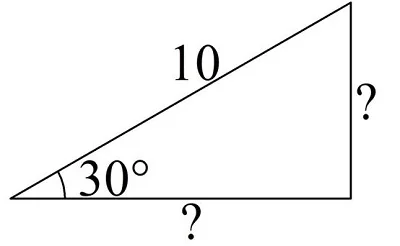
Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

10:2 = 5

Другой катет находим с помощью теоремы Пифагора:

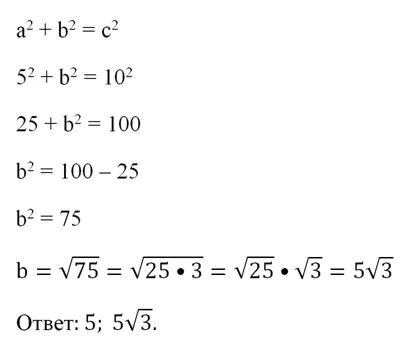
История[]

По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок». В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

Рисунок из книги Чжоу би суань цзин (500—200 лет до нашей эры)

В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков Шаблон:Донэ, приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы. В китайском сборнике задач «Математика в девяти книгах» (X—II веков Шаблон:Донэ) применению теоремы посвящена отдельная книга.

Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройкиШаблон:ПереходШаблон:Sfn, но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако, когда такие авторы, как Плутарх и Цицерон, пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненноШаблон:Sfn. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков.

Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около в 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.

Площадь равносторонних треугольников — онлайн калькулятор, формулы

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник, все стороны которого равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Площадь равностороннего треугольника по известной стороне равна произведению одной четвертой корня из трех на квадрат стороны.

Площадь равностороннего треугольника по стороне — онлайн расчет:

Формула	Результат
S = ¼ × √(3) × a²
	Сторона a (a = b = c)

Если известна высота равностороннего треугольника, то его площадь равна отношению квадрата высоты к корню из трех.

Площадь равностороннего треугольника по высоте:

Формула	Результат
S = h² ⁄ √(3)
	Высота h

Если известен радиус вписанной окружности, то площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.

Площадь равностороннего треугольника по радиусу вписанной окружности — калькулятор:

Формула	Результат
S = 3 × √(3) × r²
	Радиус r вписанной окружности

По известному радиусу описанной окружности площадь равностороннего треугольника определяется, как произведение трех четвертей корня из трех на квадрат радиуса.

Площадь равностороннего треугольника по радиусу описанной окружности:

Формула	Результат
S = ¾ × √(3) × R²
	Радиус R описанной окружности

Примечания[]

Кантор ссылается на папирус 6619 Берлинского музея
History topic: Pythagoras’s theorem in Babylonian mathematics
Шаблон:Книга
Шаблон:Cite journal: «Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики».
Шаблон:Книга
Шаблон:Cite book
Elisha Scott Loomis. Pythagorean Proposition
Euclid’s Elements: book VI, proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle».
Шаблон:Cite book
Шаблон:Cite book
Шаблон:Cite journal
Шаблон:Cite book
Шаблон:Cite book
Шаблон:Cite book
Шилов Г. Е. Математический анализ. Специальный курс. — М.: Физматлит, 1961. — C. 194
Шаблон:Cite book
Шаблон:Cite book
Шаблон:Cite book
Шаблон:Cite journal
Шаблон:Cite book
Шаблон:Cite book
Микиша А. М., Орлов В. Б. Толковый математический словарь. Основные термины. — М. Русский язык, 1989 г.
Шаблон:Cite book
Шаблон:Cite book

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка — 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√АВ 2 +√ВС 2

АС=√2474 2 +800 2 =2600 мм — все сходится.

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505 2 +√800 2 =2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

Средний уровень

Решение прямоугольного треугольника по двум сторонам

Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A), Косинус угла — cos(A), Тангенс угла — tg(A), Котангенс угла — ctg(A), Секанс угла — sec(A), Косеканс угла — cosec(A).

Решение прямоугольного треугольника

Если известны катет a и гипотенуза c

Второй катет b определится по теореме Пифагора:

Угол A определится по формуле синуса:

Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:

Если известны катеты a и b

Гипотенуза с определится по теореме Пифагора:

Угол A определится по формуле тангенса:

Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:

Пример задачи №2

Условие: вычислить диагональ, проведенную в прямоугольнике с меньшей стороной, равной 41. Если известно, что она делит угол на такие, которые соотносятся как 2 к 1.

Решение.

В этой задаче диагональ прямоугольника является наибольшей стороной в треугольнике с углом 90º. Поэтому все сводится к тому, как найти гипотенузу.

В задаче идет речь об углах. Это значит, что нужно будет пользоваться одной из формул, в которых присутствуют тригонометрические функции. А сначала требуется определить величину одного из острых углов.

Пусть меньший из углов, о которых идет речь в условии, будет обозначен α. Тогда прямой угол, который делится диагональю, будет равен 3α. Математическая запись этого выглядит так:

90º = 3 α.

Из этого уравнения просто определить α. Он будет равен 30º. Причем он будет лежать напротив меньшей стороны прямоугольника. Поэтому потребуется формула, описанная в способе №3.

Гипотенуза равна отношению катета к синусу противолежащего угла, то есть:

41 / sin 30º = 41 / (0,5) = 82.

Ответ: гипотенуза равна 82.

Пример задачи №1

Условие: в прямоугольном треугольнике проведены медианы к обоим катетам. Длина той, которая проведена к большей стороне, равна √52. Другая медиана имеет длину √73. Требуется вычислить гипотенузу.

Решение.

Так как в треугольнике проведены медианы, то они делят катеты на два равных отрезка. Для удобства рассуждений и поиска того, как найти гипотенузу, нужно ввести несколько обозначений. Пусть обе половинки большего катета будут обозначены буквой «х», а другого — «у».

Теперь нужно рассмотреть два прямоугольных треугольника, гипотенузами у которых являются известные медианы. Для них нужно дважды записать формулу теоремы Пифагора:

(2у)2 + х2 = (√52)2

(у)2 + (2х)2 = (√73)2.

Эти два уравнения образуют систему с двумя неизвестными. Решив их, легко можно будет найти катеты исходного треугольника и по ним его гипотенузу.

Сначала нужно все возвести во вторую степень. Получается:

4у2 + х2 = 52

у2 + 4х2 = 73.

Из второго уравнения видно, что у2 = 73 — 4х2. Это выражение нужно подставить в первое и вычислить «х»:

4(73 — 4х2) + х2 = 52.

После преобразования:

292 — 16 х2 + х2 = 52 или 15х2 = 240.

Из последнего выражения х = √16 = 4.

Теперь можно вычислить «у»:

у2 = 73 — 4(4)2 = 73 — 64 = 9.

у = 3.

По данным условия получается, что катеты исходного треугольника равны 6 и 8. Значит, можно воспользоваться формулой из первого способа и найти гипотенузу:

√(62 + 82) = √(36 + 64) = √100 = 10.

Ответ: гипотенуза равна 10.

Гипотенуза формула, правила и примеры вычислений

Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».

А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

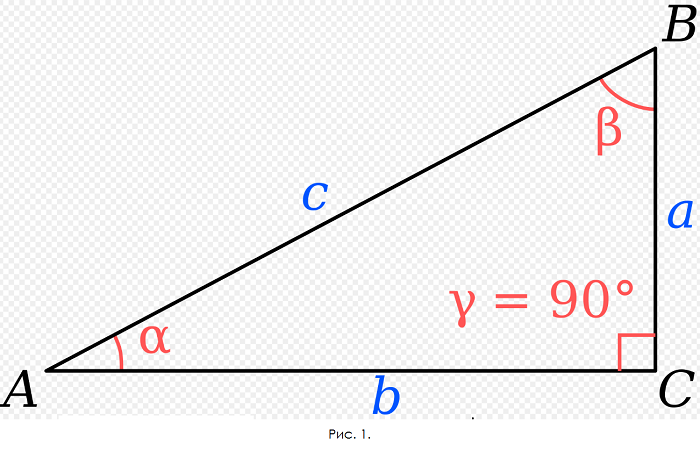
Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.

Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.

Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.

В трех измерениях

Вращающийся прямоугольный треугольник, имеющий один из катетов в качестве оси и гипотенузу в качестве образующей , образует конус с радиусом, равным неосевому катету, и высотой, равной осевому катету.

Если два подобных прямоугольных треугольника порождают два конуса при условиях предыдущего утверждения, то их объемы пропорциональны кубам любой соответствующей пары сторон. Также площади пропорциональны квадратам любой пары соответствующих сторон.

Если оба конуса имеют одну и ту же ось, а секущая плоскость, пересекающая оба конуса , образует два эллипса , то оси этих эллипсов пропорциональны друг другу (то есть они подобны).

Площадь

инжир. ar1 : Отношение между прямоугольником и двумя из трех высот (высот катетов ) прямоугольного треугольника.

Площадь прямоугольного треугольника можно рассматривать как половину площади прямоугольника, деленную на его диагональ , см . рис. ar1 ( или квадрат, если прямоугольный треугольник также ).

где a и b из уравнения ( ) представляют собой размеры двух катетов, которые совпадают с двумя сторонами и соответствующими высотами прямоугольника ( см . рис. ar1 ).

В каждом прямоугольном треугольнике каждая из двух сторон всегда равна высоте другой. Предполагая, что a = leg1 и b = leg2 , эквивалентная версия уравнения ( ) может быть записана следующим образом:

Предыдущее доказательство — это всего лишь частный, ограниченный случай гораздо более общего доказательства, справедливого для любого треугольника ( не только для прямоугольного треугольника ); И это «Предложение I.41 Евклида , которое основано на более общем понятии параллелограмма и не ограничивается прямоугольником. Это Предложение I.41 распространяет справедливость уравнения ( ) на все треугольники .

Максимальная площадь

Прямоугольный треугольник с наибольшей площадью, который можно вписать в полуокружность, — это равнобедренный прямоугольный треугольник , то есть тот, у которого равны катеты и длина , где R — радиус описанной полуокружности, а гипотенуза совпадает с диаметром.
R2{\displaystyle R{\sqrt {2}}}

Демонстрация

Работаем с полуокружностью и используем функцию площади, где основанием является гипотенуза, а высота перпендикулярна ей. Тогда ясно, что A (x) максимальна, когда h максимальна, так как 2R постоянно; Поскольку максимальное значение h получается на полуокружности, когда h = R , по симметрии предполагается, что прямоугольный треугольник равнобедренный.
A(x)=(2R)(h)2{\displaystyle A(x)={\frac {(2R)(h)}{2}}}

12 16 и 20 образуют прямоугольный треугольник?

Существует четвертая категория треугольников, в которых один из внутренних углов равен 90∘. Его называют прямоугольным треугольником. Это может быть либо разносторонний, либо равнобедренный. 1) 12,16,20: 202=162+122: Истина, следовательно, прямоугольный треугольник.

Что такое правило синуса и косинуса?

Правило синусов можно использовать для нахождения угла по 3 сторонам и углу или стороны по 3 углам и стороне. Чай правило косинуса можно найти сторону с 2-х сторон и прилежащий угол, или угол с 3-х сторон.

Как найти две недостающие стороны треугольника? Учитывая две стороны

если сторона a — недостающая сторона, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень: a = √ (c² — b²)
если нога b неизвестна, то. b = √ (c² — a²)
если гипотенуза c отсутствует, формула имеет вид. c = √ (a² + b²)

Как найти недостающую сторону треугольника по теореме Пифагора?

Площадь прямоугольного треугольника — формулы и калькуляторы

Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).

По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.

Площадь прямоугольного треугольника по двум катетам — расчет:

Формула	Результат
S = ½ × a × b
	Катет a
Катет b

Площадь прямоугольного треугольника через гипотенузу и угол:

Формула	Результат
S = ¼ × c² × sin (2α)
	Сторона c
Угол α

Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:

Формула	Результат
S = ½ × b² × tg (α)
	Сторона b
Угол α

Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:

Формула	Результат
S = d × e
	Отрезок d
Отрезок e

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:

Формула	Результат
S = r × (r + c)
	Сторона с
Радиус r

Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)

Площадь прямоугольного треугольника по формуле Герона:

Формула	Результат
S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b)
	Сторона a
Сторона b
Сторона c

Площадь треугольника — калькуляторы для всех видов

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.

Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по основанию и высоте — калькулятор онлайн:

Формула	Результат
S = ½ × a × h
	Сторона a
Высота h

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по двум сторонам и углу между ними — расчет:

Формула	Результат
S = ½ × a × b × α
	Сторона a
Сторона b
Угол α° между сторонами a и b

Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.

Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:

Формула	Результат
S = r × ½ × (a + b + c)
	Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности

Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:

Формула	Результат
S = (a × b × c) ⁄ (4 × R)
	Сторона a
Сторона b
Сторона c
Радиус R описанной окружности

Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.

Площадь треугольника по формуле Герона — калькулятор онлайн:

Формула	Результат
S = √ p × (p — a) × (p — b) × (p — c)
	Сторона a
Сторона b
Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:

Формула	Результат
S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β))
	Сторона a
Угол β°
Угол α°