Что такое медиана треугольника? ответ на webmath.ru

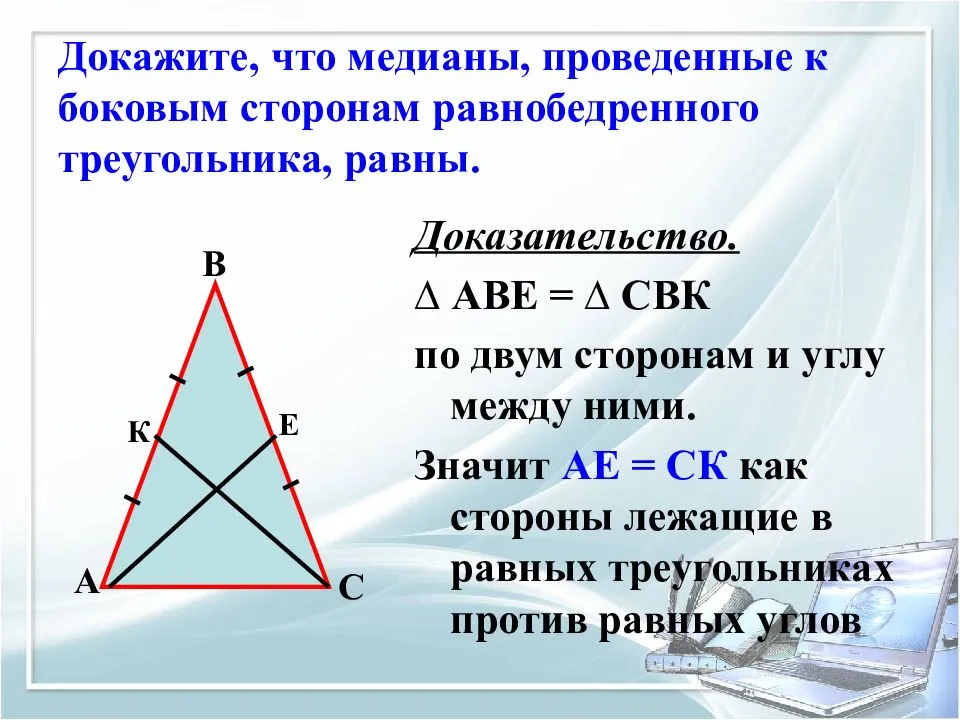
Задачи с разными видами треугольников

№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.

Решение

Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.

Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90. После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).

Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.

Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.

№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.

Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.

н = а * √3 / 2, где н — высота, а — сторона.

Подстановка и вычисление дают такой результат: н = 6 √3 (см).

Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.

Ответ: высота равна 6 √3 см.

№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.

Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.

Ответ: угол Р равен 60º.

№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.

Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º – 70º – 70º = 40º.

Ответ: углы равны 70º, 70º, 40º.

№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.

Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.

Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.

Ответ: 18º, 45º, 117º

Теорема о длине биссектрисы треугольника

Длина биссектрисы треугольника определяется по следующей формуле: где — биссектриса, проведенная к стороне — отрезки, на которые биссектриса делит сторону прилежащую к сторонам и соответственно. С доказательством этого утверждения интересующийся читатель может ознакомиться в видеоуроке.

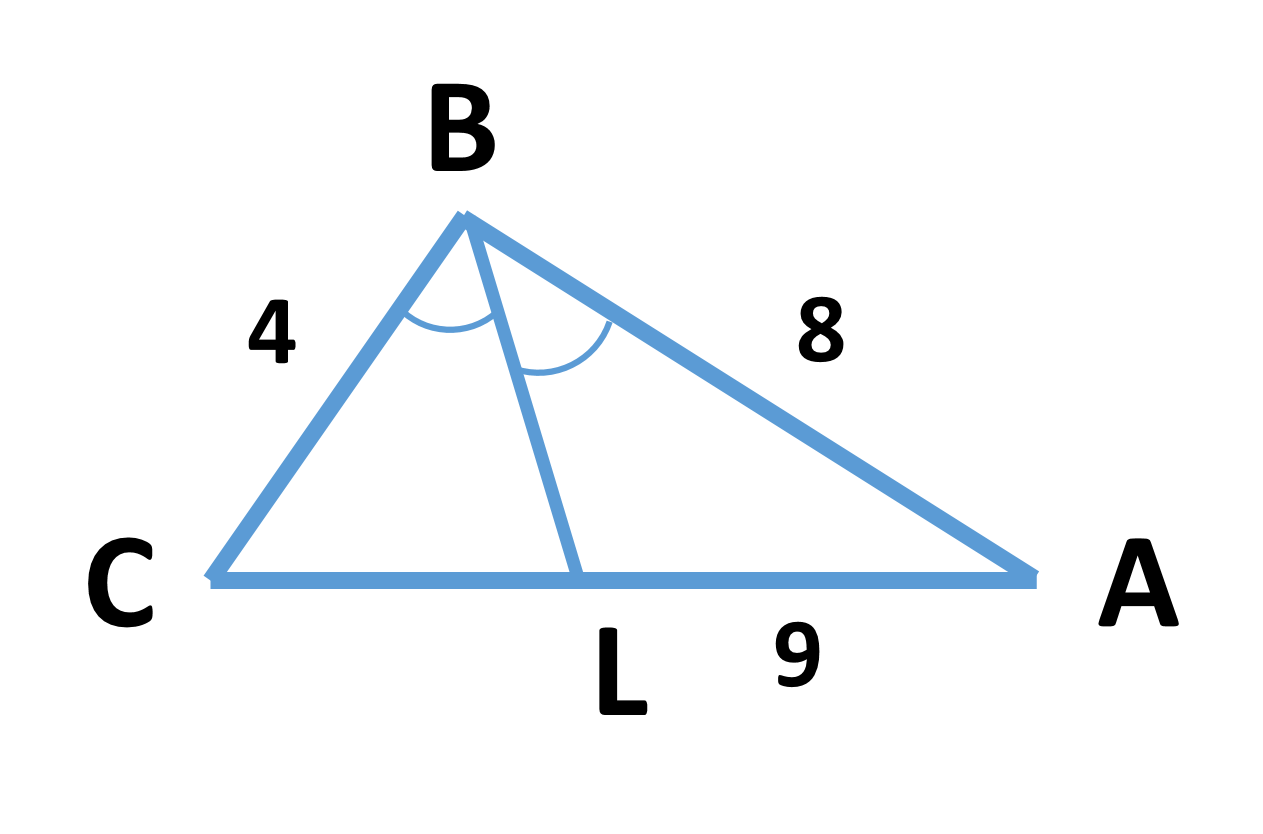
Пример 3. Дан треугольник со сторонами 4; 8; 9. Найти длину биссектрисы, проведенной к большей стороне.

Решение. Найдем сперва длины отрезков CL и LA. Используем для этого свойство биссектрисы треугольника. Биссектриса треугольника разбивает противоположную сторону на отрезки, пропорциональные прилежащим сторонам. То есть CL : CB = LA : BA или CL : 4 = LA : 8. Учитывая также, что CL + LA = 9, получаем, что CL = 3, LA = 6. По доказанной ранее теореме, длину биссектрисы BL можно найти по следующей формуле: BL2 = CB · BA — CL · LA = 4·8 — 3·6 = 14. Итак, BL =

Задача для самостоятельного решения №3. В треугольнике ABC сторона AB равна 21, биссектриса BD равна а отрезок DC равен 8. Найти периметр треугольника ABC.

Показать ответ
Ответ: 60.

Типы треугольников

Три точки, которые не лежат на одной прямой, и отрезки, которые их соединяют. Кажется, что эта фигура – самая простая

Какими могут быть треугольники, если у них всего три стороны? На самом деле вариантов довольно большое количество, и некоторым из них уделяется особое внимание в рамках школьного курса геометрии. Правильный треугольник – равносторонний, то есть все его углы и стороны равны

Он обладает рядом примечательных свойств, о которых речь пойдет дальше.

У равнобедренного равны только две стороны, и он также довольно интересен. У прямоугольного и тупоугольного треугольников, как несложно догадаться, соответственно, один из углов прямой или тупой. При этом они также могут равнобедренными.

Существует и особый вид треугольника, называемый египетским. Его стороны равны 3, 4 и 5 единицам. При этом он является прямоугольным. Считается, что такой треугольник активно использовался египетскими землемерами и архитекторами для построения прямых углов. Есть мнение, что с его помощью были возведены знаменитые пирамиды.

И все-таки все вершины треугольника могут лежать на одной прямой. В этом случае он будет называться вырожденным, в то время как все остальные – невырожденными. Именно они и являются одним из предметов изучения геометрии.

Что такое замечательные точки треугольника

Определение

Замечательные точки треугольника — это точки, расположение которых однозначно определяется треугольником и не зависит от того, в каком порядке рассматривать его стороны и углы.

Всего замечательных точек четыре. Две из них открыл Евклид, вписывая в треугольник окружности, третья, точка пересечения медиан, обнаружена Архимедом. Четвертая, в которой пересекаются высоты треугольника, не упоминалась в трудах Евклида, но описывалась в трудах его современников. Возможно, Евклид и Архимед просто упорядочили и записали доказательства теорем, известных задолго до них.

Особенность замечательных точек в том, что они в любом треугольнике являются пересечением трех линий, при этом их свойства не меняются:

биссектрисы пересекаются в центре вписанного круга;
перпендикуляры от середин сторон пересекаются в центре описанного круга;
высоты пересекаются в ортоцентре, точки, симметричные ортоцентру относительно сторон треугольника, находятся на описанном круге;
медианы пересекаются в барицентре (он же центроид, или геометрический центр).

В XVIII веке математик Леонард Эйлер, исследуя геометрию треугольников, доказал, что три из этих точек — ортоцентр, барицентр и центр описанного круга — всегда расположены на одной линии. Она называется прямой Эйлера. Точки стали называть «замечательными» или «особенными».

Треугольники
Описание	горная вершина Вершина Боковая сторона Угол На основе
Типы	Равносторонний треугольник Равнобедренный треугольник Золотой Треугольник Прямоугольный треугольник Прямой угол Катет Гипотенуза Треугольник Кеплера Тупой треугольник Острый треугольник Прямоугольник равнобедренный треугольник Псевдопрямоугольный треугольник Неравносторонний треугольник Треугольник цапли
Выдающиеся баллы ( число Кимберлинга )	Центры : Центр вписанного круга Центр гравитации Центр описанной окружности Ортоцентр Центр круга Эйлера Центр круга Шпикера Баллы Brocard Точки Фейербаха Мыс Ферма или Мыс Торричелли Лонгчамп пойнт Микель пойнт Точка Vecten Изогональные точки Точка Лемуана Точки Terquem Наполеон Очки
Замечательные линии	Cévienne Высота Медиана Посредник Brocard Right Право Эйлера Право Лемуана Линия Ньютона Линия Симсона (или линия Уоллеса) Штайнер правый Менелианский Symédiane Ортическая ось Центральный правый
Замечательные круги	Описанный круг Вписанный круг Круг Эйлера Круг Аполлония Круги Лемуана Круг Микеля Круг Тюкера Круг Брокара Круг Шпикера Круги Джонсона
Замечательные треугольники	Треугольник Морли Вписанный треугольник минимального периметра (проблема Фаньяно) Ортический треугольник
Замечательные кривые	Коническая Серре (или Макбита) вписанный конус Орто-коническая Гипербола Киперта Притчи Тритангенциальная парабола Притча о Киперте Эллипсы Мандарт Эллипс Эллипс Штейнера Эллипс Брокара Лемуанский эллипс
Теоремы	Теорема пифагора Теорема Фалеса Теорема наполеона Японская теорема Карно Теорема Менелая Теорема Морли Теорема нагеля Теорема Нойберга Теорема Гамильтона Теорема Эйлера Теорема Фейербаха Теорема Вивиани С céviennes Теорема Чевы Теорема Жергонна Теорема Стюарта Теорема теркема Теорема Рауса С кругами Теорема шести кругов Теорема Микеля о трех кругах
Отношения между треугольниками	Изометрические треугольники Подобные треугольники
разрешение	Закон косинуса Закон синусов Закон касательных Закон котангенсов Область Формула Герона

Медиана в равностороннем треугольнике свойства

Формулы. N = 2i. N — мощность алфавита (количество знаков в алфавите) i — информационный вес символа алфавита (количество информации в одном символе). I = K * i. I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения) K — число символов в.

Какие из данных утверждений верны? Запишите их номера. 1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны. 2) Диагональ трапеции делит её на два равных треугольника. 3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются Вершинами треугольника, а отрезки — его Сторонами.

Виды треугольников

Треугольник называется Равнобедренным, если у него две сторны равны. Эти равные стороны называются Боковыми сторонами, а третья сторона называется Основанием треугольника.

Треугольник, у которого все сторны равны, называется Равносторонним или Правильным.

Треугольник называется Прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется Гипотенузой, две другие стороны называются Катетами.

Треугольник называется Остроугольным, если все три его угла — острые, то есть меньше 90°.

Треугольник называется Тупоугольным, если один из его углов — тупой, то есть больше 90°.

Основные линии треугольника

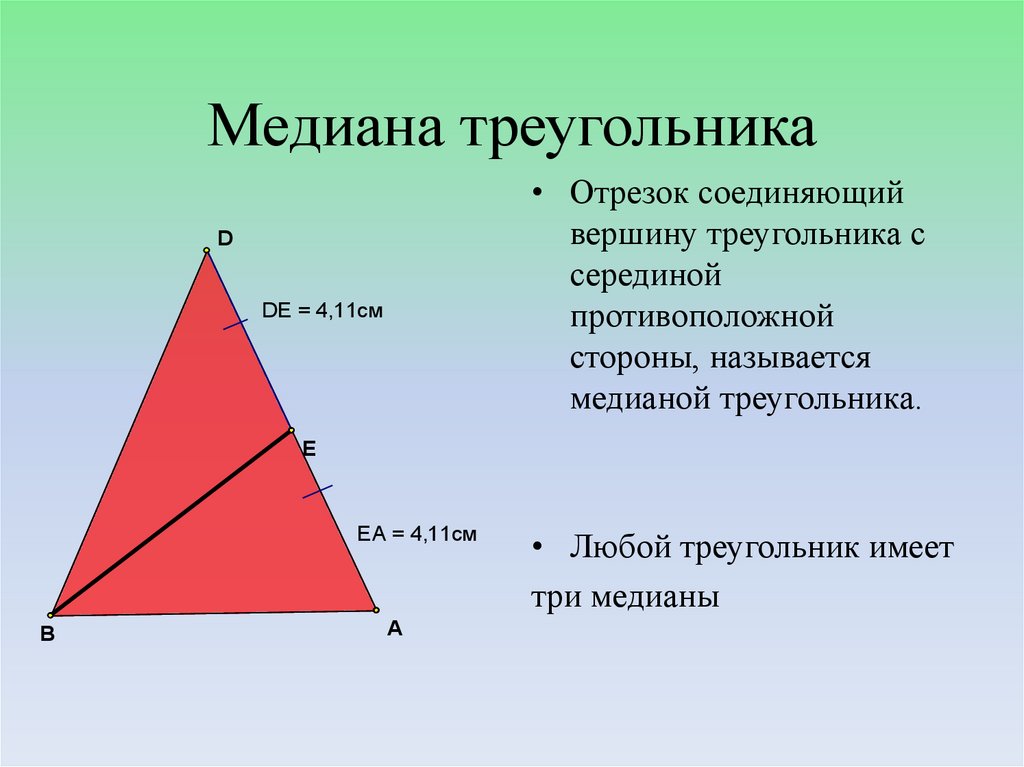
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Центром тяжести

Биссектриса

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам: . Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют Серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Признаки равенства треугольников

Два треугольника равны, если у них соответственно равны:

две стороны и угол между ними; два угла и прилежащая к ним сторона; три стороны.

Подобие треугольников

Два треугольника Подобны, если выполняется одно из следующих условий, называемых Признаками подобия:

два угла одного треугольника равны двум углам другого треугольника; две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны; три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.

В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

A 2 = B 2 + C 2 — 2Bc cos

Свойства медиан

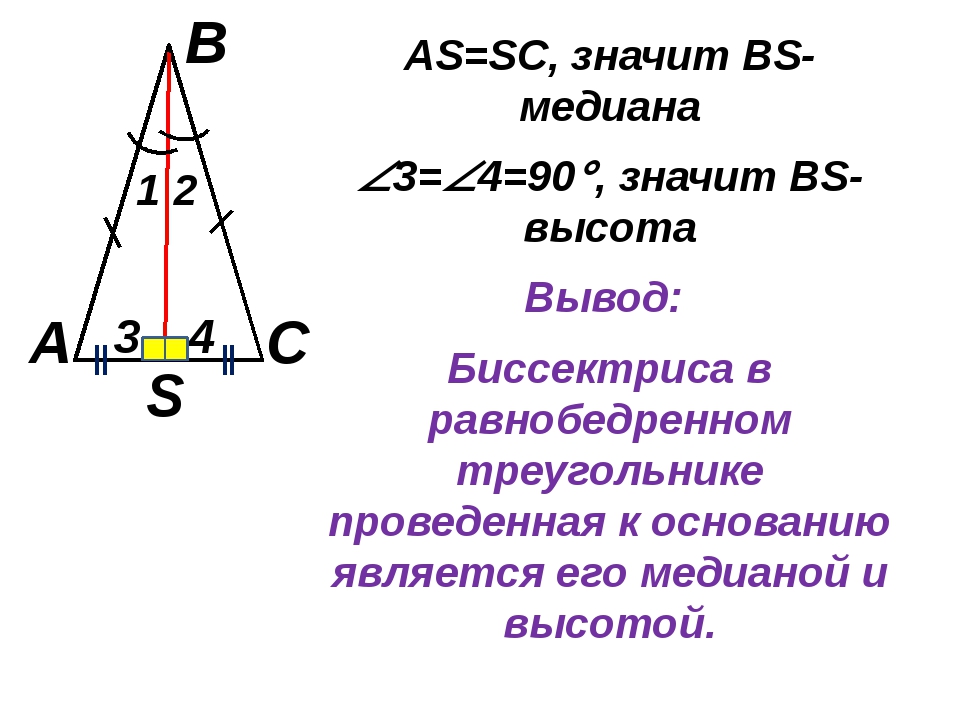
Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
Все медианы треугольника пересекаются в одной точке.
Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольника.

Равновеликими называют треугольники, площади которых равны.

Рис. 1. Три медианы образуют 6 равновеликих треугольника.

Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.

Определение медианы

Медианой треугольника называется отрезок, соединяющий один из углов треугольника с серединой противолежащей ему стороны.

(медианой также называют прямую, содержащую данный отрезок)

Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин “центроид”),
Медиана разбивает треугольник на два равновеликих треугольника.
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Большей стороне треугольника соответствует меньшая медиана.

Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.

Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)

Обозначения в формулах:

a, b – катеты прямоугольного треугольника

c – гипотенуза прямоугольного треугольника

Если обозначить треугольник, как ABC, то

ВС = а

AC = b

AB = c

(то есть стороны a,b,c – являются противолежащими соответствующим углам)

ma– медиана, проведенная к катету а

mb – медиана, проведенная к катету b

mc – медиана прямоугольного треугольника, проведенная к гипотенузе с

α (альфа) – угол CAB, противолежащий стороне а

Свойства медианы.

Какие же хорошие свойства есть у медианы?

1)
Вот представим, что треугольник — прямоугольный.
Бывают же такие, верно?

Почему??? При чём тут прямой угол?

Давай смотреть внимательно. Только не на треугольник, а на… прямоугольник. Зачем, спросишь?

А вот ты ходишь по Земле — ты видишь, что она круглая? Нет, конечно, для этого на Землю нужно смотреть из космоса. Вот и мы посмотрим на наш прямоугольный треугольник «из космоса».

Проведём диагональ:

Помнишь ли ты, что диагонали прямоугольника равны
и делятся
точкой пересечения пополам
? (Если не помнишь, загляни в тему )

Значит, половина второй диагонали — наша медиана
. Диагонали равны, их половинки, конечно же, тоже. Вот и получим

Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.

Давай посмотрим, как это свойство помогает решать задачи.

Вот, задача
:
В стороны; . Из вершины проведена медиана
. Найти, если.

Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана
равна половине стороны

Применяем теорему Пифагора:

2)
А теперь пусть у нас будет не одна, а целых три медианы
! Как же они себя ведут?

Запомни очень важный факт:

Сложно? Смотри на рисунок:

Медианы, и пересекаются в одной точке.

И….(доказываем это в , а пока запомни
!):

— вдвое больше, чем;
— вдвое больше, чем;
— вдвое больше, чем.

Не устал ещё? На следующий пример сил хватит? Сейчас мы применим всё, о чём говорили!

Задача
: В треугольнике проведены медианы и, которые пересекаются в точке. Найти, если

Найдём по теореме Пифагора:

А теперь применим знания про точку пересечения медиан.

Давай обозначим. Отрезок, а. Если не все понятно — посмотри на рисунок.

Мы уже нашли, что.

Значит, ; .

В задаче нас спрашивают об отрезке.

В наших обозначениях.

Ответ
: .

Задача про медиану в прямоугольном треугольнике

Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см. Найдите гипотенузу треугольника

Решение

Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике

В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).

Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC – общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора

AC2 + CD2 = AD2

Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то 4×2 + y2 = 9

Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC. По теореме Пифагора: EC2 + BC2 = BE2

Поскольку EC = x (медиана делит катет пополам), BC = 2y, то x2 + 4y2 = 16

Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой. Решим полученную систему уравнений. 4×2 + y2 = 9 x2 + 4y2 = 16

Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения). 5×2 + 5y2 = 25 5( x2 + y2 ) = 25 x2 + y2 = 5

Обратимся к исходному треугольнику ABC. По теореме Пифагора AC2 + BC2 = AB2

Так как длина каждого из катетов нам “известна”, мы приняли, что их длина равна 2x и 2y, то есть 4×2 + 4y2 = AB2 Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки 4 ( x2 + y2 ) = AB2 Чему равно x2 + y2 мы уже знаем (см. выше x2 + y2 = 5), поэтому просто подставим значения вместо x2 + y2

AB2 = 4 х 5 AB2 = 20 AB = √20 = 2√5

Ответ: длина гипотенузы равна 2√5

Угол между высотой и медианой треугольника |

Описание курса

Решение задачи с шестиугольной пирамидой

Предположим, что нам дана пирамида правильная с шестиугольным основанием. Известно, что высота основания пирамиды равна 13 см. Зная, что длина ее бокового ребра равна 10 см, необходимо вычислить объем и высоту правильной шестиугольной пирамиды.

Рисунок ниже показывает, как выглядит правильный шестиугольник.

Расстояние между любыми его двумя параллельными сторонами называется высотой. Не сложно показать, что эта высота ha связана с длиной стороны фигуры следующей формулой:

Подставляя в выражение значение ha, находим, что сторона основания a равна 7,51 см.

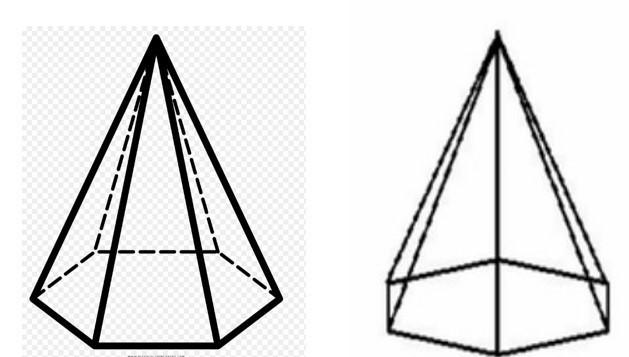
Высоту h фигуры можно определить, если рассмотреть прямоугольный треугольник, находящийся внутри пирамиды и состоящий из двух катетов (высота пирамиды и половина диагонали шестиугольного основания) и гипотенузы (боковое ребро). Тогда значение h будет равно:

Объем пирамиды определяется как третья часть от произведения высоты фигуры на площадь ее основания. Площадь правильного шестиугольника равна:

Использованная для вычисления S6 формула является универсальной для произвольного правильного n-угольника.

Для определения объема фигуры остается подставить в соответствующую формулу найденные параметры:

Мы получили значение высоты пирамиды и рассчитали ее объем. Таким образом, поставленная задача решена.

Задачи

Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:

Рис. 2. Рисунок к задаче.

Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине. Гипотенуза через теорему Пифагора: $$a^2+b^2=c^2$$

$$c=sqrt{a^2+b^2}=sqrt{9+16}=sqrt{25}=5$$

Найдем значение медианы: $$m={cover2}={5over2}=2,5$$ – получившееся число и есть значение медианы.

Значения медиан в треугольнике не равны. Поэтому нужно обязательно представлять, какую именно величину необходимо найти.

Рис. 3. Рисунок к задаче.

Чтобы решить эту задачу нужно воспользоваться одной из трех формул для нахождения медианы по сторонам треугольника:

$$m^2 ={1over2}*(a^2+c^2-b^2)$$

Как видно, главное здесь запомнить коэффициент при скобках и знаки у значения сторон. Знаки запомнить проще всего – вычитается всегда сторона, к которой опущена медиана. В нашем случае это b, но может быть любая другая.

Подставим значения в формулу и найдем величину медианы: $$m=sqrt{{1over2}*(a^2+c^2-b^2)}$$

$$m=sqrt{{1over2}*(49+81-64)}=sqrt{33}$$ – оставим результат в виде корня.

Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.

Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит в треугольнике известны основание и высота. Можно найти площадь.

$$S={1over2}*6*8=24$$

Площадь каждого из малых треугольников: $${24over6}=4$$

Что мы узнали?

Мы узнали, что такое медиана. Определили свойства медианы, и нашли решение типовых задач. Поговорили о базовых ошибках и разобрались как просто и быстро запомнить формулу нахождения медианы через стороны треугольника.

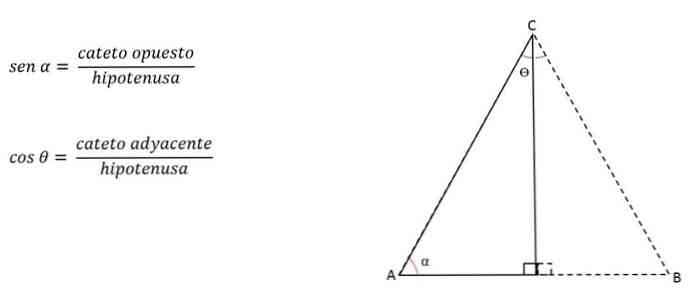
Как рассчитать высоту?

Поскольку высота — это линия, перпендикулярная основанию, она делит ее на две равные части, продолжаясь до противоположной вершины. Таким образом образуются два равных прямоугольных треугольника.

Высота (h) представляет противоположную сторону (a), половину стороны AC относительно соседней стороны (b), а сторона BC представляет гипотенузу (c).

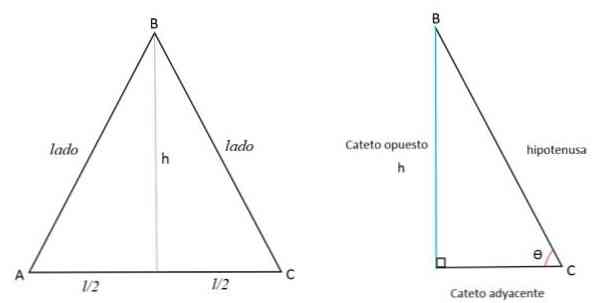
Используя теорему Пифагора, вы можете определить значение высоты:

в2 + б2= с2

где:

в2 = высота (ч).

б2 = сторона б / 2.

с2 = сторона а.

Подставляя эти значения в теорему Пифагора, и очищая высоту, мы имеем:

час2 + ( л / 2)2 = L2

час2 + L24 = L2

час2 = L2 — L24

час2 = (4_*L2 — L2) 4

час2 = 3_*L24

√час2 = √ (3_*L24)

Если угол, образованный конгруэнтными сторонами, известен, высоту (представленную ногой) можно рассчитать, применяя тригонометрические соотношения.

Ноги называются противоположными или смежными в зависимости от угла, взятого за основу.

Например, на предыдущем рисунке катет h будет противоположен углу C, но прилегает к углу B:

Таким образом, высота может быть рассчитана с помощью: