Равнобедренный треугольник

Нахождение сторон прямоугольного треугольника

1

Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам.

Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата, а не в виде кривой, которая обозначает непрямые углы.

В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.
2

Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла).
3

Определите, какую сторону треугольника требуется найти. Теорема Пифагора позволяет найти любую сторону прямоугольного треугольника (если известны две другие стороны). Определите, какую сторону (a, b, c) необходимо найти.
- Например, дана гипотенуза, равная 5, и дан катет, равный 3. В этом случае необходимо найти второй катет. Мы вернемся к этому примеру позднее.
- Если две другие стороны неизвестны, необходимо найти длину одной из неизвестных сторон, чтобы иметь возможность применить теорему Пифагора. Для этого используйте основные тригонометрические функции (если вам дано значение одного из непрямых углов).
4

Подставьте в формулу a2 + b2 = c2 данные вам значения (или найденные вами значения).

В нашем примере напишите: 3² + b² = 5².

Помните, что a и b — это катеты, а с — гипотенуза.
5

Возведите в квадрат каждую известную сторону.

В нашем примере напишите: 9 + b² = 25.

Или же оставьте степени — вы можете возвести числа в квадрат позже.
6

Обособьте неизвестную сторону на одной стороне уравнения.

В нашем примере перенесите 9 на правую сторону уравнения, чтобы обособить неизвестное b². Вы получите b² = 16.

Для этого перенесите известные значения на другую сторону уравнения. Если вы находите гипотенузу, то в теореме Пифагора она уже обособлена на одной стороне уравнения (поэтому делать ничего не нужно).
7

Извлеките квадратный корень из обеих частей уравнения.

В нашем примере b² = 16. Извлеките квадратный корень из обеих частей уравнения и получите b = 4. Таким образом, второй катет равен 4.

На данном этапе на одной стороне уравнения присутствует неизвестное (в квадрате), а на другой стороне — свободный член (число).
8

Используйте теорему Пифагора в повседневной жизни, так как ее можно применять в большом числе практических ситуаций. Для этого научитесь распознавать прямоугольные треугольники в повседневной жизни — в любой ситуации, в которой два предмета (или линии) пересекаются под прямым углом, а третий предмет (или линия) соединяет (по диагонали) верхушки двух первых предметов (или линий), вы можете использовать теорему Пифагора, чтобы найти неизвестную сторону (если две другие стороны известны).
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
  - «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
    - a² + b² = c²
    - (5)² + (20)² = c²
    - 25 + 400 = c²
    - 425 = c²
    - с = √425
    - с = 20,6. Таким образом, приблизительная длина лестницы равна 20,6 метров.

Равнобедренный треугольник: определение

Однако мы не о строительстве. Если присмотреться к древнеегипетским пирамидам как прежде всего к геометрическим фигурам, мы заметим, что грани пирамиды представляют собой треугольники. Довольно интересной формы.

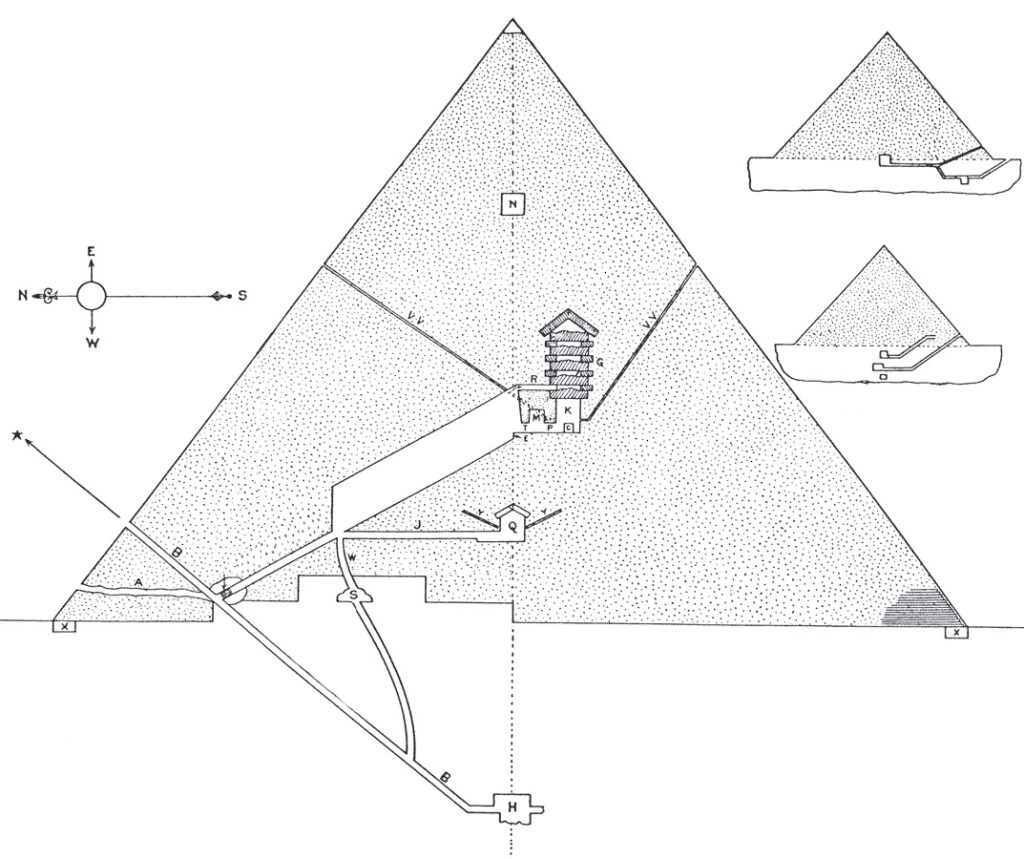
Обратите внимание на схематичное изображение Пирамиды Хеопса в поперечном разрезе. В треугольнике подобном гранями пирамид Древнего Египта боковые стороны являются равными по величине

Это — частный случай геометрии треугольников, который мы с вами сегодня и будем разбирать.

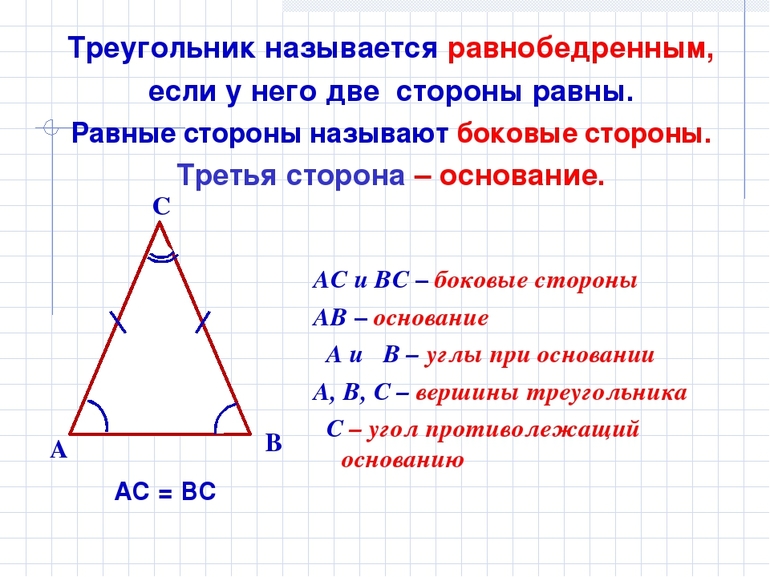
Значит, равнобедренный треугольник имеет равные «бедра» — боковые стороны при основании. На чертеже такой треугольник изображен и размечен отдельно. Посмотрите: в $\bigtriangleup{ABC}$ имеется основание $AB$ и боковые стороны $BC$ и $CA$, при этом $BC=CA$.

Рисуйте правильно!

В случае с треугольником с произвольно заданными сторонами и углами особой роли не играет, как вы разместите его на чертеже. Можно под углом, можно основанием параллельно к краю листа.

Равнобедренный треугольник? Наоборот: крайне важно располагать его по принципу грани древнеегипетской пирамиды — основанием к «земле», то есть к низу, не под углом

{"questions":[{"content":"Если в треугольнике равны не только боковые стороны, но и боковые стороны равны основанию, можно ли назвать такой треугольник равнобедренными? `choice-1`","widgets":{"choice-1":{"type":"choice","options":,"explanations":["","","Так держать! Треугольник, в котором равны все стороны, считается равнобедренным, ведь боковые стороны в нем равны. Однако при равенстве трех сторон корректнее употреблять термин «равносторонний». О треугольниках с равными сторонами поговорим отдельно чуть позже."],"answer":}}}]}

Задача. Дан равнобедренный треугольник $\bigtriangleup{ABC}$. Основание $AB$ больше боковой стороны на $2~см$, но меньше суммы боковых сторон на $3~см$. Найдите стороны треугольника.

РешениеОбозначим боковую сторону треугольника как $y$, а основание как $x$. Согласно условию, можно записать два следующих уравнения:

$$x=y+2,\\x=2y-3$$

Подставим во второе уравнение вместо $x$ правую часть первого уравнения и вычислим значение боковой стороны: $2+y=2y-3.$ Откуда получаем значение $y$ равное $5$. В равнобедренном треугольнике боковые стороны равны, поэтому значение второй стороны также будет равняться $5$.

Далее подставляем полученное значение в первое уравнение и находим основание: $$x=y+2=7$$

Ответ: $5, 5, 7.$

Признаки равнобедренной фигуры

Существует 4 явления, с помощью которых можно определить принадлежность тела к треугольникам. Все они сгруппированы в 3 теоремы:

Если в треугольнике построить медиану, при этом она будет совпадать с высотой, он является равнобедренным. Аналогично можно утверждать о принадлежности фигуры к равнобедренному типу, когда биссектриса совпадает с высотой.
Если 2 угла равны, треугольник равнобедренный.
Если медиана и биссектриса совпадают, причём построены из одного угла, фигура называется равнобедренной.

Для доказательства первой теоремы нужно использовать признаки равенства треугольников. Если изобразить на чертеже фигуру ABC и из вершины B построить высоту, согласно заданным данным, она будет медианой или биссектрисой. В первом случае противоположная сторона будет разделена на 2 равные части AD и DC. Значит, треугольники ABD и DBC одинаковые. Отсюда следует, что у фигур есть равные стороны: AB = BC., то есть боковые грани имеют одинаковую длину, что и требуется по определению.

Доказательство второй теоремы следует построить на нахождении равных сторон. Для этого нужно отложить серединный перпендикуляр a и доказать, что линия будет проходить через вершину B. Если она не будет пересекать угол B, она касается AB или BC. Пусть точкой пересечения перпендикуляра будет M. Тогда по первому признаку AKM = CKM, значит, углы MCK и MAK также равны. По условию теоремы MCK = MAB → MAK = MAB, что противоречит аксиоме измерения углов. Отсюда можно утверждать, что серединный перпендикуляр не пересекает BC или AC. Значит, прямая проходит через вершину B.

Общие сведения

Замкнутую фигуру, состоящую из трёх пересекающихся прямых и такого же количества внутренних углов, называют треугольником. Отрезки, которые соединяют точки, образующие фигуру, называют сторонами. Для обозначения используют малые латинские буквы. Точка, в которой соединяется 2 стороны, называется вершиной. Её принято подписывать заглавными буквами, например, A, B, C.

Существует несколько видов фигур по типу углов и по длинам сторон:

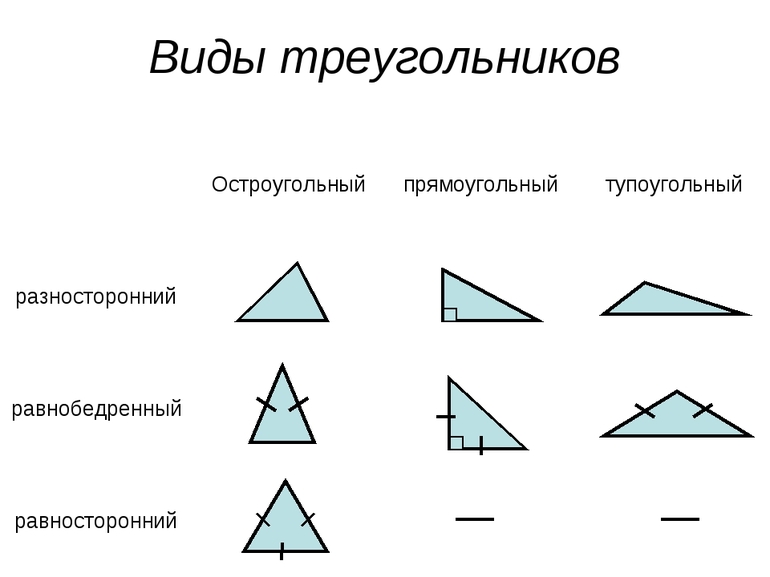
разносторонние — все отрезки, образующие многоугольник, имеют различную длину;
равнобедренные — 2 стороны одинаковы;
равносторонние — все 3 стороны равны;
остроугольными — 3 угла многоугольника являются острыми;
прямоугольными — 2 стороны образуют угол в 90 градусов;
тупоугольными — размер одного угла превышает 90 градусов.

Прежде всего это медиана — отрезок, построенный из вершины к центру противолежащей стороны, разделяющий фигуру на 2 равных треугольника. Биссектрисой называют линию, построенную к противоположной стороне и разделяющую угол на 2 равные части. Также можно опустить перпендикуляр на любую сторону из вершины. Называют такую линию высотой.

В треугольнике можно провести по 3 любых таких линии. Причём точка пересечения отрезков имеет своё название: 3 высоты встречаются в ортоцентре, а биссектрисы — инцентре. Если в треугольник вписать окружность, её центр совпадёт с местом пересечения медиан. Эта точка является центроидом, центром массы фигуры. Кроме этого, можно описать круг, в центре которого будут пересекаться серединные перпендикуляры.

Свойства равнобедренного треугольника

Доказательство. Дан равнобедренный треугольник $\bigtriangleup{ABC}$ с основанием $AB$. По определению $BC=CA$. Проведем в треугольнике биссектрису $CD$ к основанию и рассмотрим треугольники $\bigtriangleup{ADC}$ и $\bigtriangleup{DBC}$.

Они равны по первому признаку равенства треугольников, то есть по двум сторонам и углу между ними: $BC=CA,$ $\angle{DCA}=\angle{BCD},$ биссектриса $CD$ — общая сторона. Если треугольники равны, то против равных сторон в них будут лежать равные углы. Откуда делаем вывод, что $\angle{CAB}=\angle{ABC}$. Теорема равнобедренного треугольника доказана.

Мы помним, что периметр — сумма всех сторон треугольника. Равнобедренный треугольник — равные стороны при основании, так что для случая с таким треугольником формулу периметра можно немного «подлатать»: $P=2a+b$, где $a$ — длина боковой стороны, $b$ — длина основания.

{"questions":}

Медианы, биссектрисы, высоты и равнобедренный треугольник

На чертеже равнобедренного треугольника выше внимание привлекает вот что: биссектриса равнобедренного треугольника как будто бы является одновременно и высотой в треугольнике, и медианой. На самом деле нам не кажется

Одно из главных свойств равнобедренных треугольников заключается в том, что проводя, к примеру, медиану, вы получаете в то же самое время высоту и биссектрису равнобедренного треугольника. И это все один отрезок. Сформируем на основе наших предположений теорему и докажем ее

На самом деле нам не кажется. Одно из главных свойств равнобедренных треугольников заключается в том, что проводя, к примеру, медиану, вы получаете в то же самое время высоту и биссектрису равнобедренного треугольника. И это все один отрезок. Сформируем на основе наших предположений теорему и докажем ее.

Доказательство

Дан равнобедренный треугольник $\bigtriangleup{ABC}$. К основанию $AB$ проведена медиана $CD$. Треугольники $\bigtriangleup{ADC}$ и $\bigtriangleup{DBC}$ будут равны по первому признаку треугольников: $\angle{CAB}$ и $\angle{ABC}$ равны по теореме об углах равнобедренного треугольника, стороны $BC$ и $CA$ равны по определению равнобедренного треугольника, $AD=DB$ по определению медианы.

Из равенства треугольников следует равенство углов $\angle{ACD}$ и $\angle{BCD}$. Тогда $CD$ — биссектриса. Углы $\angle{ADC}$ и $\angle{BDC}$ равны из доказанного равенства треугольников $\bigtriangleup{ADC}$ и $\bigtriangleup{DBC}$. Эти углы являются смежными.

Раз сумма смежных углов равна $180^{\circ}$ и углы при этом равны, то они оба равняются $90^{\circ}$. Из этого следует, что $CD$ — высота. Теорема доказана.

Совет!

Eсли проводите в равнобедренном треугольнике, скажем, медиану, сразу отмечайте на чертеже свойство высоты и биссектрисы.

Или в любом другом порядке, в зависимости от того, что за отрезок требуется в условии. Это поможет постоянно иметь перед глазами свойства равнобедренного треугольника, что значительно облегчит доказательство утверждения или решение задачи.

{"questions":[{"content":"Надеемся, что вы не забыли между делом про существование равносторонних треугольников — тех, в которых равны не только боковые стороны, но вообще все стороны. Будет ли биссектриса равностороннего треугольника являться и медианой, и высотой, если она проведена к боковой стороне, а не к основанию? `choice-1`","widgets":{"choice-1":{"type":"choice","options":,"explanations":,"answer":}}}]}

Решение задач

Рассмотрим следующие задачи:

Пример 1 На рисунке АВ = ВС, ∠1 = . Найдите ∠2.

Решение Выполним пояснительный рисунок:

Рис. 4. Чертеж к примеру 1

1. ∠АСВ = – = (по свойству смежных углов). Значит, угол при основании равнобедренного треугольника равен .

2. ∠ВАС = ∠АСВ = (поскольку углы при основании равнобедренного треугольника равны).

3. ∠2 = ∠ВАС (как вертикальные), значит, ∠2 = ∠ВАС = .

Ответ:.

Пример 2 Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника ВСD равен 45 см. Найдите стороны АВ и ВС.

Дано: АВ = АС, ВС = СD = DB. = 40 см. = 45 см.

Найти: АВ и ВС.

Решение Выполним пояснительный рисунок:

Рис. 5. Чертеж к примеру 2

Решение: Пусть ВС = х, тогда все стороны равностороннего треугольника тоже равны х. Пусть АВ = у, тогда обе боковые стороны треугольника равны у. Следуя условию, 3х = 45. Найдем х. х = 45 : 3 = 15. Используем факт, что = 40 см. 15 + 2у = 40, 2у = 25, у = 25 : 2 = 12,5.

Ответ: АВ = 12,5 см, ВС = 15 см.

Пример 3: Медиана АМ в треугольнике АВС равна отрезку ВМ. Докажите, что ∠ВАС = ∠В + ∠С.

Дано: ВМ = МС, АМ = ВМ.

Доказать: ∠ВАС = ∠В + ∠С.

Доказательство: Выполним пояснительный рисунок:

Рис. 6. Чертеж к примеру 3

Треугольник АМВ – равнобедренный, углы при основании равны, значит, ∠1 = ∠2. треугольник АМС – равнобедренный, значит, углы при основании равны, ∠4 = ∠3.

∠1 + ∠4 = ∠2 + ∠3

∠ВАС = ∠В + ∠С

Ответ: Доказано.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/7-klass/treugolnikib/reshenie-zadach-po-teme-ravnobedrennyy-treugolnik

https://www.youtube.com/watch?v=TyOhs9-_-3M

http://istudy.su/wp-content/uploads/2013/03/4_Ravnobedrennyj-treugolnik-732×1024.jpg

http://school-assistant.ru/?predmet=geometr&theme=ravnobedrennij_treugolnik

http://greatschool.ru/files/tasks/1577/121041.gif

http://blogstudy.ru/gdzimg/214aaa/20111205125802.jpeg

http://www.flconf.org/education/wp-content/uploads/2011/04/5107103-1886×2550-1-1024×757.jpg

http://cs1-26v4.vk-cdn.net/p15/f1c21f09bd9fad.mp3?extra=u96JCzuBb-XdruFah977CJD_izMWWpkY6XMumaQX91DaN6oYjpkhgbiIWHT_JgbeMV8sBTXjR7DNV22iBzUUOuBrsARIHPev

http://nsportal.ru/sites/default/files/2015/01/31/priznaki_ravenstva_treugolnikov.rar

Домашнее задание

1. Дайте определение равнобедренного треугольника.
2. В чем особенность этого треугольника?
3. Чем отличается равнобедренный треугольник от прямоугольного?
4. Назовите известные вам свойства равнобедренного треугольника.
5. Как вы думаете, можно ли на практике проверить равенство углов при основании и как это сделать?

Задание

А теперь давайте проведем небольшой блиц-опрос и узнаем, как вы усвоили новый материал.

Послушайте внимательно вопросы и ответьте верно ли такое утверждение, что:

1. Треугольник можно считать равнобедренным, если у него две стороны равны?
2. Биссектрисой называют отрезок, который соединяет вершину треугольника с серединой противоположной стороны?
3. Биссектрисой является отрезок, который делит угол, который соединяет вершину с точкой противоположной стороны пополам?

Советы относительно решения задач о равнобедренном треугольнике:

1. Для определения периметра равнобедренного треугольника достаточно умножить длину боковой стороны на 2 и сложить это произведение с длиной основы треугольника.
2. Если в задаче известны периметр и длина основы равнобедренного треугольника, то для нахождения длины боковой стороны достаточно отнять длину основы от периметра и найденную разницу разделить на 2.
3. А чтобы найти длину основы равнобедренного треугольника, зная и периметр, и длину боковой стороны, необходимо всего лишь умножить боковую сторону на два и отнять это произведение от периметра нашего треугольника.

Задачи:

1. Среди треугольников на рисунке определите один лишний и объясните свой выбор:

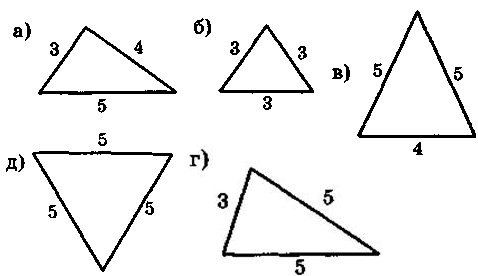
2. Определите, какие из изображенных на рисунке треугольников являются равнобедренными, назовите их основы и боковые стороны, а так же рассчитайте их периметр.

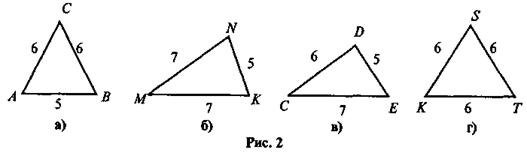
3. Периметр равнобедренного треугольника равен 21 см. Найдите стороны этого треугольника, если одна из них больше на 3 см. Какое количество решений может иметь данная задача?

4. Известно, что если боковая сторона и противолежащий основе угол одного равнобедренного треугольника равен боковой стороне и углу другого, то эти треугольники будут равны. Докажите это утверждение.

5. Подумайте и скажите, является ли любой равнобедренный треугольник равносторонним? И будет ли любой равносторонний треугольник равнобедренным?

6. Если стороны равнобедренного треугольника равны 4 м и 5 м, то каков будет его периметр? Сколько решений может иметь эта задача?

7. Если один из углов равнобедренного треугольника равен 91 градусу, то чему равны остальные углы?

8. Подумайте и ответьте, какие углы должны быть у треугольника, чтобы он одновременно был и прямоугольным, и равнобедренным?

История теоремы

Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.

Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.

Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.

Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.

Свойства и признаки равнобедренного треугольника

О нас

Демоверсии

Учебные пособия

Справочник по математике

Геометрия (Планиметрия)

Треугольники

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Равнобедренный треугольник		Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Свойство	Углы при основании равнобедренного треугольника		Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Признак	Два равных угла треугольника	Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Свойство	Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника		В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.
Признак	Высота треугольника, совпадающая с медианой		Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Признак	Высота треугольника, совпадающая с биссектрисой		Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Признак	Биссектриса треугольника, совпадающая с медианой		Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным

Определение: равнобедренный треугольник
	Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.
Свойство: углы при основании равнобедренного треугольника
	Если треугольник является равнобедренным треугольником, то углы при его основании равны.
Признак: два равных угла треугольника
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.
Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.
Признак: высота треугольника, совпадающая с медианой
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным
Признак: высота треугольника, совпадающая с биссектрисой
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным
Признак: биссектриса треугольника, совпадающая с медианой
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным

Определение равнобедренного треугольника

Определение:
Равнобедренным треугольником называют треугольник, у которого две стороны равны.
Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.

Свойство углов при основании равнобедренного треугольника

Свойство:Если треугольник является равнобедренным треугольником, то углы при его основании равны.

Признак равнобедренного треуголька: два равных угла треугольника

Признак:Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником.

Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника

Свойство:В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.

Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой

Признак:Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным

Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой

Признак:Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным

Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой

Признак:Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Другие свойства равнобедренного треугольника

Положение центра окружности, описанной вокруг равнобедренного треугольника, зависит от величины угла вершины. Так, если равнобедренный треугольник остроугольный, центр круга располагается внутри фигуры.

Центр окружности, которая описана вокруг тупоугольного равнобедренного треугольника, лежит вне его. И, наконец, если величина угла при вершине равна 90°, центр лежит ровно на середине основания, а через само основание проходит диаметр окружности.

Для того чтобы определить радиус окружности, описанной около равнобедренного треугольника, достаточно разделить длину боковой стороны на удвоенный косинус половины величины угла при вершине.