Таблица примеров
Проверьте на рабочем листе книги Excel следующие примеры. Чтобы все заработало корректно, вам необходимо использовать смешанную ссылку при копировании формулы. Закрепите номер столбца, содержащего возводимое число, и номер строки, содержащей показатель. Ваша формула должна иметь примерно следующий вид: «=$B4^C$3».
|
Число / Степень |
|||||
Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях. Не возникает проблем и с возведением любых чисел в целые показатели
А вот возведение отрицательного числа в дробную степень обернется для вас ошибкой, поскольку невозможно выполнить правило, указанное в начале нашей статьи про возведение отрицательных чисел, ведь четность — это характеристика исключительно ЦЕЛОГО числа.
Начальный уровень
Степень и ее свойства. Исчерпывающий гид (2019)
Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?
Чтобы узнать все о степенях, о том для чего они нужны, как использовать свои знания в повседневной жизни читай эту статью.
И, конечно же, знание степеней приблизит тебя к успешной сдаче ОГЭ или ЕГЭ и к поступлению в ВУЗ твоей мечты.
Let»s go… (Поехали!)
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Для этого нужно нажать CTRL+F5 (на Windows) или Cmd+R
(на Mac).
Стандартный вид числа
В физике и других естественных науках изучаются объекты, чьи характеристики (масса, длина, скорость и т.д.) могут измеряться очень большими или очень малыми величинами. Например, масса атома железа равна 0,0000000000000000000000000927 килограмм, а масса Солнца оценивается в 1988500000000000000000000000000 килограмм. Работать с такими числами достаточно неудобно. Сложно даже сравнивать их между собой, ведь для этого надо подсчитывать количество нулей в каждом числе. Поэтому в науке часто используется особая форма чисел, которую называют стандартным видом числа. Он основан на том, что любое число можно записать как произведение числа a, находящегося в пределах от 1 до 10, и какой-нибудь целой (в том числе отрицательной) степени десятки.

Приведем примеры представления чисел в стандартном виде
90 = 9•10 = 9•101
91 = 9,1•10 = 9,1•101
900 = 9•100 = 9•102
912 = 9,12•100 = 9,12•102
Покажем случаи, когда порядок равен нулю или меньше него
7 = 7•1 = 7•10
7,63 = 7,63•1 = 7,63•10
0,8 = 8•0,1 = 8•10– 1
0,0875 = 8,75•100 = 8,75•10– 2
Посмотрите, насколько короче выглядит запись физических величин с использованием стандартного вида:
- масса Солнца: 1988500000000000000000000000000 кг = 1,9885•1030 кг;
- масса Земли: 5970000000000000000000000 кг = 5,97•1024 кг;
- масса атома железа: 0,0000000000000000000000000927 = 9,27•10-26 кг.
Пример. Укажите стандартный вид числа 76000000.
Решение. Первой ненулевой цифрой в записи является семерка, поэтому стандартный вид будет выглядеть так:
7,6•10n
где n– какое-то целое число, которое нам надо найти. Поставим в исходном числе запятую после семерки:
7,6000000
Видно, что мы отделили запятой 7 разрядов, то есть перенесли запятую на 7 разрядов вправо. Поэтому n равно 7:
76000000 = 7,6•107
Действительно, умножение дробного числа на 10 приводит к смещению запятой на одну позицию влево, поэтому при умножении 7,6 на 107 получим 76000000. Наши действия можно проиллюстрировать рисунком:
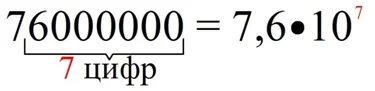
В случае с числами, меньшими единицы, также надо смотреть на количество разрядов между запятой и первой ненулевой цифрой. Пусть надо представить в стандартном виде десятичную дробь 0,000005605. Значащей частью числа будет 5,605. Для того чтобы получить ее, надо в исходной дроби перенести запятую на 6 разрядов вправо. Поэтому порядок будет равен (– 6):
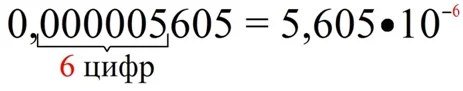
Теперь попробуем выполнить обратное преобразование – по стандартному виду числа записать его в привычной нам десятичной форме. Пусть есть запись 2,56•105. Для начала искусственно припишем несколько ноликов к значащей части:
2,56 = 2,5600000
Теоретически мы можем дописать любое количество нулей, величина дроби от этого не изменится. Порядок числа равен 5, а потому запятую надо перенести на 5 знаков вправо:
2,5600000•105 = 256000,00
Теперь лишние нули после запятой и саму запятую можно и убрать:
256000,00 = 256000
Обратите внимание, что порядок числа был равен 5, а в итоге мы получили шестизначное число. Можно сформулировать правило: у числа, имеющего в стандартной виде порядок n, в десятичной представлении перед запятой будет стоять (n + 1)знак
Например:
1,23456789•106 = 1234567,89
Здесь порядок числа равен 6, а потому перед запятой стоит 7 знаков.
Напомним, что если число целое и, соответственно, в его записи нет запятой, то ее можно искусственно добавить:
568 = 568,0
Теперь рассмотрим похожий пример с отрицательным порядком числа. Пусть надо записать в десятичном виде число 9,8765•10– 4. Для этого сначала можно условно «подрисовать» нолики перед значащей частью:
0000009,8765
Порядок равен (– 4), а потому надо передвинуть запятую на 4 знака влево
0000009,8765 =000,00098765
Получается, что мы подрисовали слишком много ноликов. Уберем два из нихи получим число в обычной форме:
0,00098765
Вообще, если у числа отрицательный порядок (– n), то первая ненулевая цифра должна оказаться на n-ой позиции после запятой:
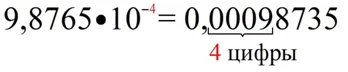
Возведение в степень: определение
Возведение числа в натуральную степень — это умножение его на само себя определенное количество раз. Это такая же операция в алгебре, как сложение, вычитание, умножение или деление.
Если определенное число нужно умножить на себя несколько раз, это значит, что его необходимо возвести в соответствующую степень. Например, если четыре нужно умножить само на себя три раза, это равно тому, что четыре следует возвести в третью степень. Закодировать это выражение можно следующей арифметической записью:
43, где 4 — это основание, а 3 — показатель. Также 43 = 4·4·4 = 64
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Основные правила выполнения данных вычислений:
- итог возведения отрицательного основания в четную степень — положительный;
- итог возведения отрицательного основания в нечетную — отрицательный;
- итог возведения положительного основания в любую — положительный;
- любое основание с показателем один равно себе;
- ноль при любом возведении в результате дает ноль;
- единица с любым показателем равна единице;
- любое основание с показателем ноль равно единице.
Таблица представляет собой ряд чисел, возведенных в определенные степени.
Парадокс нуля
Здесь все гораздо сложнее, но не настолько, чтобы не разобраться. Известно, что 0x = 0. Например: 04 = 0 × 0 × 0 × 0 = 0 Почему же мы часто встречаем выражение 0 = 1? На самом деле это не совсем верно. Возьмем функцию y = ƒ (x) = xx. Подберем значения по табл.1.
Таблица 1. Функция ƒ(x) = xx
| x | xx |
| 1 | 1 |
| 0,9 | 0,909 |
| 0,8 | 0,836 |
| 0,7 | 0,779 |
| 0,6 | 0,736 |
| 0,5 | 0,707 |
| 0,4 | 0,693 |
| 0,3 | 0,697 |
| 0,2 | 0,725 |
| 0,1 | 0,794 |
| 0,01 | 0,955 |
| 0,001 | 0,993 |
Как видим, с определенного момента значение xx растет вместе с уменьшением x. В этом нет ничего сверхъестественного, это всего лишь пример действия формулы
Изобразим это на графике
Рис.1 График y = ƒ(x) = xxТаким образом, делаем предположение, что это выражение является пределом.
Проверим, вычислив это значение. Преобразуем основание выражения. Получаем:
xx = (eln x)x = ex ln x
В этом случае x → 0, а ln x → -∞ Получаем следующее выражение:
Пользуемся правилом Лопиталя:
Получаем:
Доказательство получено. Официальная позиция современной математики гласит, что выражение 0– представляет собой неопределенность, то есть не имеет точного значения. Однако на практике, при расчетах, его значение подстраивается под конкретные требования. И чаще всего в этих случаях оно равно единице. Чтобы лучше разобраться с темой нулевой степени, советуем посмотреть видео ниже.
Свойства степеней с рациональными показателями
мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковыми основаниями при a>0, а если и , то при a≥0;
- свойство частного степеней с одинаковыми основаниями при a>0;
- свойство произведения в дробной степени при a>0 и b>0, а если и , то при a≥0 и (или) b≥0;
- свойство частного в дробной степени при a>0 и b>0, а если , то при a≥0 и b>0;
- свойство степени в степени при a>0, а если и , то при a≥0;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a<b и рациональном p при p>0 справедливо неравенство ap<bp, а при p<0 – неравенство ap>bp;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq.
Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: 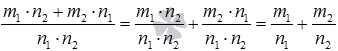 . На этом доказательство завершено.
. На этом доказательство завершено.
Абсолютно аналогично доказывается второе свойство степеней с дробными показателями: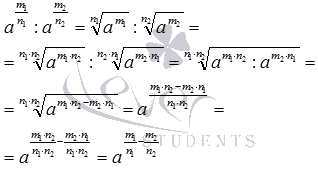
По схожим принципам доказываются и остальные равенства:
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b, a<b и рациональном p при p>0 справедливо неравенство ap<bp, а при p<0 – неравенство ap>bp. Запишем рациональное число p как m/n, где m – целое число, а n – натуральное. Условиям p<0 и p>0 в этом случае будут эквивалентны условия m<0 и m>0 соответственно. При m>0 и a<b по свойству степени с целым положительным показателем должно выполняться неравенство am<bm. Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, ap<bp.
Аналогично, при m<0 имеем am>bm, откуда , то есть, и ap>bp.
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq. Мы всегда можем привести к общему знаменателю рациональные числа p и q, пусть при этом мы получим обыкновенные дроби и , где m1 и m2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m1>m2, что следует из . Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0<a<1 должно быть справедливо неравенство am1<am2, а при a>1 – неравенство am1>am2. Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq.
Действия со степенями: правила вычисления степеней с разными основаниями или натуральными показателями по математике и порядок этого
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом: an = a * a * a * …an.
Причем, левая часть уравнения будет читаться, как a в степ. n.
Например:
- 23 = 2 в третьей степ. = 2 * 2 * 2 = 8,
- 42 = 4 в степ. два = 4 * 4 = 16,
- 54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625,
- 105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000,
- 104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- an * am = (a)(n+m),
- an : am = (a)(n-m),
- (ab ) m=(a)(b*m).
Проверим на примерах:
23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично:
- 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
- (23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
33 + 24 = 27 + 16 = 43,
52 – 32 = 25 – 9 = 16
Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.. Как производить вычисления в более сложных случаях? Порядок тот же:
Как производить вычисления в более сложных случаях? Порядок тот же:
- при наличии скобок – начинать нужно с них,
- затем возведение в степень,
- потом выполнять действия умножения, деления,
- после сложение, вычитание.
Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: am/n.
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Действия с числами в стандартном виде
Стандартный вид чисел удобен тогда, когда есть необходимость сравнивать физические величины, а также перемножать их и делить. Рассмотрим правила сравнения умножения и деления чисел в стандартном виде.
Из двух чисел больше то, у которого больше порядок стандартного вида числа. Так, масса Солнца больше масса Земли, так как у нее порядок равен 30, а у нашей планеты – только 24. Если же порядки одинаковы, то больше то число, у которого больше значащая часть.
Пример. Радиус ядра Солнца оценивается в 1,73•108 м, а радиус Юпитера составляет 6,99•107 м. Какая из этих величин больше?
Решение. Порядок у радиуса ядра Солнца равен 8, а у Юпитера только 7, поэтому радиус ядра Солнца больше радиуса Юпитера.
Пример. Масса протона составляет 1,673•10– 27 кг, а масса нейтрона равна 1,675•10– 27 кг. Какая из этих двух частиц тяжелее?
Решение. У обоих величин одинаковый порядок, равный (– 27). Однако значащая часть у массы нейтрона больше:
1,675 > 1,673
Следовательно, нейтрон тяжелее.
Ответ: Нейтрон тяжелее.
Посмотрим, как перемножать числа, находящиеся в стандартном виде. Переставляя множители местами, можно получить:
(a•10n)•(b•10m) = a•b•10n•10m = (ab)•10n+m
В итоге можно сформулировать правило:

Пример. Земля двигается по своей орбите со средней скоростью 3•104 м/с. Какое расстояние она проходит в течение одного невисокосного календарного года (в каждом таком году 31536000 секунд)?
Решение. Переведем количество секунд в году в стандартный вид
31536000 = 3,1536 •107
Расстояние (обозначим его как S) равно произведению средней скорости на время:
S = 3•104 м/с • 3,1536•107c = 3•3,1536•104 + 7 = 9,4608•1011м.
Ответ: 9,4608•1011м.
Пример. Представьте в стандартном виде произведение чисел 9,5•108 и 1,38•10– 2.
Решение.
(9,5•108)•(1,38•10– 2) = (9,5•1,38)•108 + (– 2) = 13,11•106
Получили число НЕ в стандартном виде, так как 13,11 > 10. Поэтому следует произвести замену 13,11 = 1,311•10:
13,11•106 = 1,311•10•106 = 1,311•107
Ответ: 1,311•107
Теперь попытаемся поделить два числа, находящихся в стандартном виде:
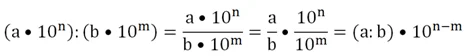
Видно, что справедливо следующее правило:

Пример. Во сколько раз масса Солнца больше массы Земли?
Решение. Выше мы приводили данные, что масса Солнца оценивается в 1,9885•1030 кг, а масса нашей планеты составляет 5,97•1024 кг. Поделим массу звезды на массу планеты:
(1,9885•1030):(5,97•1024) = (1,9885:5,97)•1030 – 24≈0,333•106 = 333000
Получили, что Солнце примерно в 333 тысячи раз тяжелее Земли.
Ответ: В 333000 раз.
Степень с натуральным показателем, квадрат числа, куб числа
Для начала дадим определение степени числа с натуральным показателем. Забегая вперед, скажем, что определение степени числа a с натуральным показателем n дается для действительного числа a, которое будем называть основанием степени, и натурального числа n, которое будем называть показателем степени. Также отметим, что степень с натуральным показателем определяется через произведение, так что для понимания нижеизложенного материала нужно иметь представление об умножении чисел.
Определение.
Степень числа a с натуральным показателем n – это выражение вида an, значение которого равно произведению n множителей, каждый из которых равен a, то есть, .В частности, степенью числа a с показателем 1 называется само число a, то есть, a1=a.
Из данного определения понятно, что с помощью степени с натуральным показателем можно кратко записывать произведения нескольких одинаковых множителей. Например, 8·8·8·8 можно записать как степень 84. Это аналогично тому, как с помощью произведения записывается сумма одинаковых слагаемых, к примеру, 8+8+8+8=8·4 (смотрите статью общее представление об умножении натуральных чисел).
Сразу стоит сказать о правилах чтения степеней. Универсальный способ чтения записи an таков: «a в степени n». В некоторых случаях также допустимы такие варианты: «a в n-ой степени» и «n-ая степень числа a». Для примера возьмем степень 812, это «восемь в степени двенадцать», или «восемь в двенадцатой степени», или «двенадцатая степень восьми».
Вторая степень числа, а также третья степень числа имеют свои названия. Вторую степень числа называют квадратом числа, например, 72 читается как «семь в квадрате» или «квадрат числа семь». Третья степень числа называется кубом числа, к примеру, 53 можно прочитать как «пять в кубе» или сказать «куб числа 5».
Пришло время привести примеры степеней с натуральными показателями. Начнем со степени 57, здесь 5 – основание степени, а 7 – показатель степени. Приведем еще пример: десятичная дробь 4,32 является основанием, а натуральное число 9 – показателем степени (4,32)9.
Обратите внимание, что в последнем примере основание степени 4,32 записано в скобках: чтобы избежать разночтений мы будем брать в скобки все основания степени, которые отличны от натуральных чисел. В качестве примера приведем следующие степени с натуральными показателями , их основания не являются натуральными числами, поэтому они записаны в скобках
Ну и для полной ясности в этом моменте покажем разницу, заключенную в записях вида (−2)3 и −23. Выражение (−2)3 – это степень отрицательного числа −2 с натуральным показателем 3, а выражение −23 (его можно записать как −(23)) соответствует числу, противоположному значению степени 23.
Заметим, что встречается обозначение степени числа a с показателем n вида a^n. При этом, если n – многозначное натуральное число, то показатель степени берется в скобки. Например, 4^9 – это другая запись степени 49. А вот еще примеры записи степеней при помощи символа «^»: 14^(21), (−2,1)^(155). В дальнейшем мы преимущественно будем пользоваться обозначением степени вида an.
Данное выше определение позволяет находить значение степени с натуральным показателем. Для этого нужно вычислить произведение n одинаковых множителей, равных a. Эта тема заслуживает детального рассмотрения в отдельной статье – смотрите возведение в степень с натуральным показателем.
Одной из задач, обратной возведению в степень с натуральным показателем, является задача нахождения основания степени по известному значению степени и известному показателю. Эта задача приводит к понятию корня из числа.
Также стоит изучить свойства степени с натуральным показателем, которые вытекают из данного определения степени и свойств умножения.
Как пользоваться таблицей степеней числа два?
Первый столбец – это степень двойки, который одновременно, обозначает число бит, которое представляет число.
Второй столбец – значение двойки в соответствующей степени (n).
Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) – это 128
Третий столбец – максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).
Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число – это ноль, то максимальное число, которое можно представить с помощью семи бит 128 – 1 = 127 . Это и есть значение третьего столбца.
| Степень двойки (n) | Значение степени двойки 2n |
Максимальное число без знака, записанное с помощью n бит |
Максимальное число со знаком,
записанное с помощью n бит |
| 1 | – | – | |
| 1 | 2 | 1 | – |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | 3 |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 17 | 131 072 | 131 071 | 65 535 |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 67 108 863 | 33 554 431 |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | 268 435 455 |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных
Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения “плюс/минус”. Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Для этого же самого примера ( 27) семью битами можно записать максимум число +63, поскольку один бит занят знаком “плюс”. Но мы можем хранить и число “-63“, что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.
Степень с целым показателем
После того как мы определили степень числа a с натуральным показателем, возникает логичное стремление расширить понятие степени и перейти к степени числа, показателем которой будет любое целое число, в том числе и отрицательное и нуль. Это следует делать так, чтобы оставались справедливыми все свойства степени с натуральным показателем, так как натуральные числа являются частью целых чисел.
Степень числа a с целым положительным показателем есть не что иное как степень числа a с натуральным показателем: , где n – целое положительное число.
Теперь определим нулевую степень числа a. Будем исходить из свойства частного степеней с одинаковыми основаниями: для натуральных чисел m и n, m<n и отличного от нуля действительного числа a выполняется равенство am:an=am−n (условие a≠0 необходимо, так как в противном случае мы бы имели деление на нуль). При m=n записанное равенство нас приводит к следующему результату an:an=an−n=a. Но с другой стороны an:an=1 как частное равных чисел an и an. Следовательно, приходится принять a=1 для любого отличного от нуля действительного числа a.
А как же быть с нулем в нулевой степени? Подход, примененный в предыдущем абзаце, не подходит для этого случая. Можно вспомнить про свойство произведения степеней с одинаковыми основаниями am·an=am+n, в частности при n=0 имеем am·a=am (из этого равенства тоже видно, что a=1). Однако, при a=0 мы получим равенство 0m·0=0m, которое можно переписать как 0=0, оно верно при любом натуральном m вне зависимости от того, чему равно значение выражения 0. Иными словами, 0 может быть равно любому числу. Чтобы избежать этой многозначности, не будем приписывать нулю в степени нуль никакого смысла (по этим же соображениям при изучении деления мы не стали придавать смысл выражению 0:0).
Несложно проверить, что принятое нами равенство a=1 для отличных от нуля чисел a согласуется со свойством степени в степени (am)n=am·n. Действительно, при n=0 имеем (am)=1 и am·0=a=1, а при m=0 имеем (a)n=1n=1 и a0·n=a=1.
Так мы пришли к определению степени с нулевым показателем. Степень числа a с нулевым показателем (a отличное от нуля действительное число) равна единице, то есть, a=1 при a≠0.
Приведем примеры: 5=1, (33,3)=1, , а 0 – не определено.
Нулевую степень числа a определили, осталось определить целую отрицательную степень числа a. В этом нам поможет все то же свойство произведения степеней с одинаковыми основаниями am·an=am+n. Примем m=−n, что требует условия a≠0, тогда a−n·an=a−n+n=a=1, откуда заключаем, что an и a−n – взаимно обратные числа. Таким образом, логично определить число a в целой отрицательной степени −n как дробь . Несложно проверить, что при таком задании степени отличного от нуля числа a с целым отрицательным показателем остаются справедливыми все свойства степени с натуральным показателем (смотрите свойства степени с целым показателем), к чему мы и стремились.
Озвучим определение степени с целым отрицательным показателем. Степень числа a с целым отрицательным показателем −n (a отличное от нуля действительное число) – это есть дробь , то есть, при a≠0 и натуральном n.
Рассмотрим данное определение степени с целым отрицательным показателем на конкретных примерах: 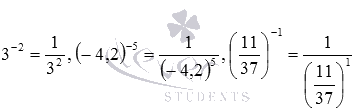 .
.
Подытожим информацию этого пункта.
Определение.
Степень числа a с целым показателем z определяется так:


































